Aula 03 – Complexidade de fibonacci recursiva simples

Voltar para página principal do blog

Todas as aulas desse curso

Aula 02           Aula 04

Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook

Esse é o link do código fluente no Pinterest

Meus links de afiliados:

Hostinger

Digital Ocean

One.com

Meu github:
https://github.com/toticavalcanti

Vamos ver um exemplo bem simples de otimização do algoritmo.

É um algoritmo para somar os n números.

Por exemplo, se eu chamar a função soma passando 5:

soma(5)

Ela deve me retornar 15, pois 0 + 1 + 2 + 3 + 4 + 5 = 15

Vamos a implementação menos eficiente, mais ingênua.

Utilizaremos python para ilustrar:

#O(n)
def sum_slow(n):
    s = 0
    for n in range(n + 1):
        s += n
    return s
def main():
    n = int(input())
    print( sum_slow(n) )
if __name__ == "__main__":
    main()

A complexidade desse algoritmo acima é O(n)

Quem não souber o que significa: if __name__ == "__main__":no código acima, assista a Aula 13 – Python – Modules – Módulos – Código Fluente. 😉

Será que existe uma implementação melhor, mais eficiente do que essa?

Vamos tentar reduzir a complexidade para O(1)!

#O(1)
def sum_fast(n):
    return n * (n + 1) // 2
def main():
    n = int(input())
    print( sum_fast(n) )
if __name__ == "__main__":
    main()

Veja que nesse caso ele não precisou fazer loop, apenas a conta, por isso, a complexidade O(1).

Sequência de Fibonacci

Vamos a um outro exemplo, agora um pouco mais complexo, utilizaremos recursividade.

Recursividade

De acordo com o wikipedia, recursividade é a definição de uma sub-rotina (função ou método) que pode invocar a si mesma.

Vamos trabalhar com a famosa, curiosa, misteriosa… sequência de Fibonacci.

Fibonacci, também conhecido como Leonardo de Pisa, ou ainda Leonardo Bigollo, foi um matemático italiano da República de Pisa, considerado “o mais talentoso matemático ocidental da Idade Média.

A sequência foi descrita por ele no ano de 1202, através do crescimento de uma população de coelhos, embora a sequência já fosse conhecida na antiguidade.

A famosa seqüência cativou matemáticos, artistas, designers e cientistas por séculos.

É também conhecida como a proporção áurea, sua onipresença e funcionalidade surpreendente na natureza sugere sua importância como uma característica fundamental do universo.

A sequência começa com 0 e 1, depois, os números subsequentes são compostos pela soma dos dois números anteriores da sequência.

(n – 1) + (n – 2) = próximo número da sequência.

Então a sequência dos 8 primeiros números da sequência é: 0, 1, 1, 2, 3, 5, 8, 13, 21

Exemplos na natureza

Pétalas de flores

Pétalas de flores

O número de pétalas em uma flor segue a seqüência de Fibonacci.

Os exemplos famosos incluem o lírio, que tem três pétalas, ranúnculos, que têm cinco (foto acima), a chicória, 21, a margarida, 34, e assim por diante.

Cabeça de uma flor

Cabeça de uma flor

A cabeça de uma flor também está sujeita aos processos de Fibonacci, normalmente as sementes são produzidas no centro e em seguida, migram para o exterior para preencher todo o espaço.

Os girassóis fornecem um ótimo exemplo desses padrões em espiral.

Galhos de árvores

Galhos de árvores

A seqüência de Fibonacci também pode ser vista no modo como os galhos das árvores se formam ou se separam.

Um tronco principal crescerá até produzir um ramo, que cria dois pontos de crescimento.

Então, um dos novos ramos ramifica-se em dois, enquanto o outro fica dormente.

Esse padrão de ramificação é repetido para cada uma das novas hastes.

Caracol

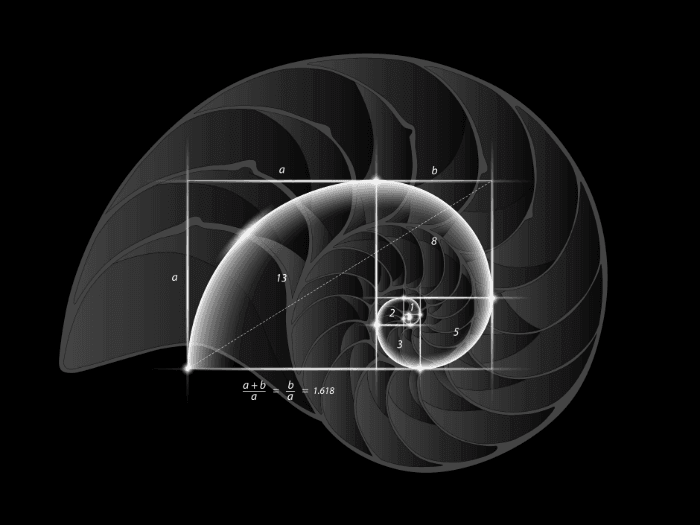
Caracol

Veja na figura acima a sequência descrita com os números da sequência dentro do caracol.

Fica muito clara a sequência nele.

As propriedades exclusivas do Retângulo Dourado fornecem outro exemplo.

É retângulo no qual a proporção dos lados a / b é igual à média dourada (phi), resultando em um processo de aninhamento que pode ser repetido infinitamente e que assume a forma de uma espiral.

É chamado de espiral logarítmica e é abundante na natureza.

Galáxias espirais

Galáxias espirais

As galáxias espirais também seguem o padrão de Fibonacci.

A Via Láctea tem vários braços espirais, cada um deles uma espiral logarítmica de cerca de 12 graus.

Como vimos, a sequência de Fibonacci está muito presente na natureza, em obras de artes, etc.

Tá presente desde o nível quântico até corpos celestes inimaginavelmente grandes.

Face Humana

Face humana

Faces, humanas e não humanas, abundam com exemplos da Proporção Áurea.

A boca e o nariz estão posicionados em seções douradas da distância entre os olhos e a parte inferior do queixo.

Proporções semelhantes podem ser vistas de lado, e até mesmo o olho e a própria orelha (que segue ao longo de uma espiral).

Enfim, são muitos os exemplos ao nosso redor.

Então vamos lá, vamos ao algoritmo!

Primeiro vamos a implementação recursiva simples, a menos eficiente.

#Recursiva, complexidade O(2^n)
def fib(n):
    #custo da operação de comparação <= é de 1
    if n <= 1: 
        return n
    else:
        #custo de cada chamada é 1, por causa das operações de subtração
        #e o custo da soma também é 1, totalizando 3 de custo
        return fib(n-1) + fib(n-2)

Análise da complexidade:

T(n) = T(n – 1) + T(n – 2) + 4 (4 é a soma dos custos vistos acima no código).

T(0) = T(1) = 1 (porque para no if)

Vamos imaginar que T(n – 1) e T(n – 2) tenha aproximadamente a mesma complexidade.

T(n – 1) ≈ T(n – 2)

O que vamos fazer é encontrar o limite inferior e superior de T(n), isto é, o limite inferior e superior de fib(n).

Na verdade o tempo para calcular T(n – 1) é maior do que para calcular T(n – 2) porque n – 1 é maior que n – 2. Confira no grafo mais abaixo: Grafo das chamadas recursivas da função fib().

c = 4 (constante)

T(n) = 2T(n – 2) + c

O c acima, é que estamos considerando o 4, que é a soma dos custo das operações, como uma constante.

T(n) = 2T(n – 2) + c, pode ser rescrito assim:

T(n) = 2{ 2T(n – 4) + c } + c

T(n) = 4T(n – 4) + 3c            // k = 2

T(n) = 8T(n – 6) + 7c            // k = 3

T(n) = 16T(n – 8) + 15c        // k = 4

T(n) = 2^k * T(n – 2k) + (2^k – 1)c

O caso base T(0) e T(1) é uma operação que leva tempo constante.

T (0) = T (1) = 1 

Então para encontrar o k usaremos o T(0) em:

T(n) = 2^k * T(n – 2k) + (2^k – 1)c

Por isso, n – 2k = 0 para termos T(0).

n – 2k = 0

k = n/2

Então:

T(n) = 2^n/2 * T(0) + (2^n/2 – 1)c

T(n) ≈ 2^n/2 (Limite inferior)

Vamos fazer a mesma coisa com T(n) = 2T(n – 1) + c

c = 4 (constante)

T(n) = 2T(n – 1) + c

T(n) = 4T(n – 2) + 3c

T(n) = 8T(n – 3) + 7c

T(n) = 2^kT(n – k) + (2^k – 1)c

Para T(0) temos que:

n – k = 0

n = k

T(n) = 2^n * T(0) + (2^n – 1) * c

T(n) = 2^n * 1 + (2^n – 1) * c

T(n) ≈ 2^n (Limite superior)

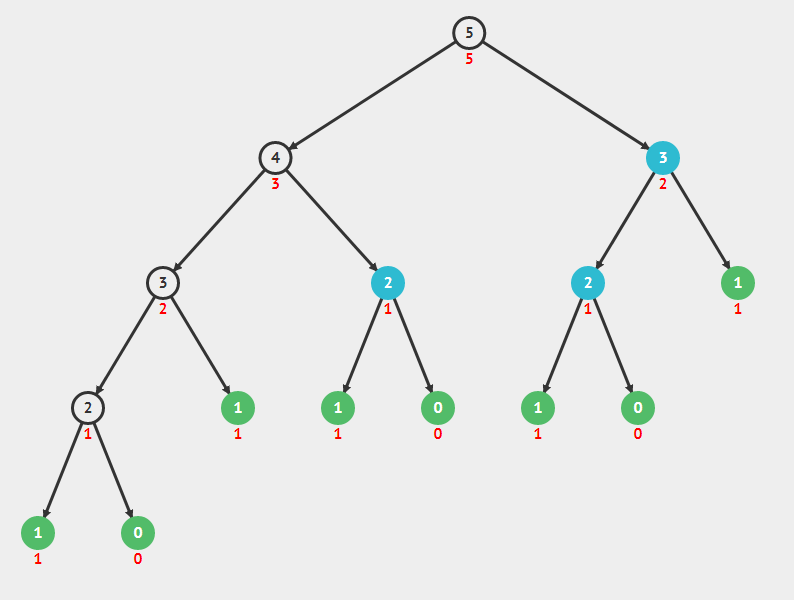
Grafo das chamadas recursivas da função fib()

Você pode pensar assim, na série => 0 1 1 2 3, em que n = 5, supondo que você comece de n = 0.

Leva menos tempo para obter n = 3 que é avaliado como 1 do que para obter n = 4 que é avaliado para 2.

Com complexidade de O(2^n/2), para o limite inferior e O(2^n) para o limite superior.

No final das contas, podemos dizer que a complexidade é de O(2^n).

Na próxima aula, faremos uma outra implementação recursiva, mas, que reduzirá a complexidade para O(n^2), complexidade exponencial, para uma complexidade linear, O(n).

Aproveitaremos para falar de uma técnica chamada programação dinâmica.

Ficamos por aqui, até mais. 🙂

Aula 02           Aula 04

Todas as aulas desse curso

Voltar para página principal do blog

Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook

Esse é o link do código fluente no Pinterest

Meus links de afiliados:

Hostinger

Digital Ocean

One.com

Meu github:

https://github.com/toticavalcanti

Obrigado, até a próxima e bons estudos. 😉