Aula 02 – Tensor Flow – Redes Neurais no Colab
Aula 02 – Tensor Flow – Redes Neurais no Colab
Voltar para página principal do blog
Todas as aulas desse curso
Aula 01 Aula 03
Meu github:
https://github.com/toticavalcanti
Documentação oficial do TensorFlow:
https://www.tensorflow.org/
Link para o notebook da aula:
notebook-da-aula

Python com Tensorflow
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Link do código fluente no Pinterest
Aproveito para deixar meus link de afiliados:
Hostinger
Digital Ocean
One.com
Aula 02 – Tensor Flow – Redes Neurais no Colab
Para aula prática, vamos utilizar o google colab.
Google Colab
O google colab é uma ferramenta gratuita, que nos permite escrever, rodar e compartilhar código com o google drive.
Dentro do colab a ferramenta utilizada é o Jupyter, que fornece um ambiente de desenvolvimento interativo para notebooks Jupyter na web.
Na aula 3 do curso de computação quântica aqui do código fluente, eu mostro como instalar o anaconda, ele vem com várias ferramentas legais, entre elas o Jupyter, que você pode rodar localmente.
No nosso caso aqui, iremos utilizar a versão online do Jupyter, portanto só é preciso ter uma conta no google.
Como toda a estrutura do ambiente fica na nuvem do google, você não precisa instalar nada na sua máquina local.
Jupyter Notebook
O Jupyter Notebook é um aplicativo web de código aberto que permite criar e compartilhar documentos que contêm código ativo, equações, visualizações e texto narrativo.
Os usos incluem: limpeza e transformação de dados, simulação numérica, modelagem estatística, visualização de dados, aprendizado de máquina e muito mais.
Como falamos na aula passada, um Tensor consiste de um vetor de n dimensões, é a estrutura de dados
básica utilizada pelo TensorFlow.
Um Grafo de computação é a malha que consistem em nós conectados entre si por arestas.
Cada nó tem entradas e saídas, assim como a operação que deve ser feita com as entradas para que as saídas sejam criadas.
As arestas consistem nos valores que são passados de um nó para outro.
Cada nó realiza a determinada operação assim que recebe todos os inputs necessários.
Sessões
Os nós do grafo podem ser agrupados em sessões.
Cada sessão pode ser executada separadamente em threads ou até mesmo em forma de computação distribuída.
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
a = tf.constant([ [1.0, 2.0], [3.0, 4.0] ])
b = tf.constant([ [5.0, 6.0], [7.0, 8.0] ])
c = tf.matmul(a,b)
sess = tf.Session()
print(sess.run(c))
#Saída:
#[[19. 22.]
# [43. 50.]]Placeholders
Placeholders são tensores indefinidos, os quais receberão um valor posteriormente.
Eles são úteis para receber as amostras de entrada e a saída que serão utilizadas no
grafo de computação da rede neural.
Vamos criar um placeholder do tipo float com dimensão 3×3.
Em seguida usar a biblioteca Numpy para gerar um tensor 3×3 com valores aleatórios.
Em seguida criamos a sessão e o grafo é executado.
Note que dessa vez o parâmetro feed_dict é explicitamente definido.
Esse parâmetro recebe como valor um dict que possui como chave o placeholder criado, e como valor o array de valores aleatório chamado rand_array.
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
a = tf.compat.v1.placeholder(tf.compat.v1.float32 , shape=(3,3))
b = tf.compat.v1.matmul(a,a)
rand_array = np.random.rand(3,3)
sess = tf.Session()
result = sess.run(b, feed_dict={a: rand_array})
print(result)
#Saída:
#[[0.71275765 0.27279112 0.2693102 ]
# [1.1098326 0.54741037 0.49013594]
# [1.6771501 0.7718581 0.84457034]]
Redes Neurais
A ideia das redes neurais é utilizar um sistema computacional inspirado em como a comunicação entre os neurônios do cérebro fazem para processar informações.
É um processamento paralelamente distribuído constituído de unidades de processamento simples, os nós.
Esses nós na computação equivaleriam ao nosso neurônio.
Até antes de 2006, não era possível treinar redes neurais para superar técnicas de aprendizado de máquina mais tradicionais, como por exemplo, SVM, árvore de decisão.
As redes neurais profundas é o principal modelo para tarefas de classificação que estão relacionadas as áreas de visão computacional, reconhecimento de fala e processamento de linguagem natural.
Perceptron
O Perceptron foi inventado em 1957 por Frank Rosenblatt, é a estrutura
mais básica de uma Rede Neural.
A Figura abaixo mostra a estrutura de um Perceptron.
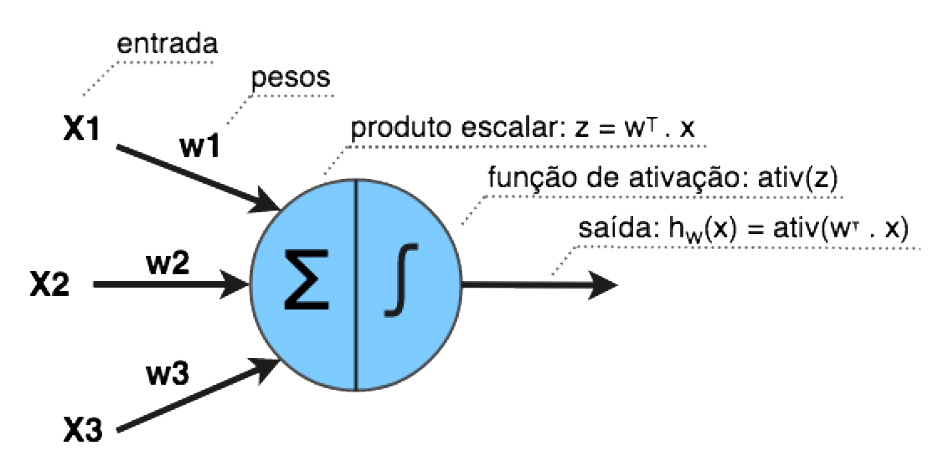
Perceptron
Cada entrada x possui um peso w associado.
Em seguida é feito o cálculo do produto escalar entre os dados de entrada e seus pesos.
Z = W1X1 +W2X2 +…+WnXn = Wt . X)
Depois uma função de ativação é aplicada no produto escalar, resultando na saída do perceptron:
aw(X) = ativ(Z) = ativ(Wt . X)
É comum utilizar uma entrada com valor constante 1 para representar o viés (em inglês, bias) do neurônio.
Em fontes mais recentes, o viés é considerado, por padrão, um dado interno do neurônio, resultando na equação:
Z = Wt . X+b
Podemos usar vários Perceptrons para realizar tarefas de múltipla classificação.
A rede A mostra os neurônios organizados em paralelo e cada um fica responsável por aprender a ativar para uma classe específica.
A classe predita é selecionada ao usar a função argmax para obter a maior ativação, ou seja, a maior recompensa dentre todas as saídas dos neurônios.
Esse modelo é chamado de Perceptron Multiclasse.
Na rede B, os neurônios estão também estruturados em múltiplas camadas, onde cada neurônio das camadas intermediarias (ou escondida) é conectado com todos os neurônios da camada anterior.
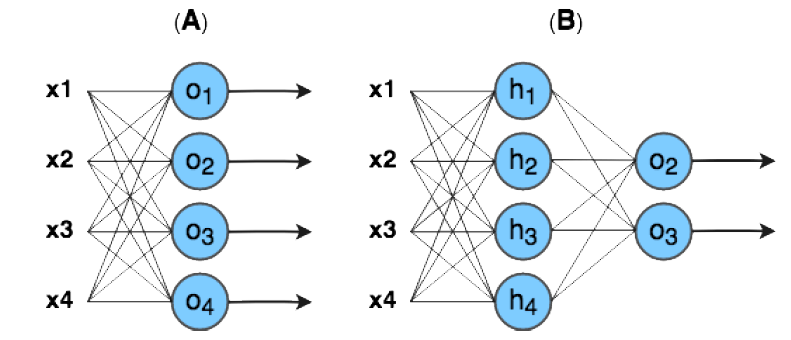
A Perceptron Multiclasse e B Perceptron múltiplas camadas
Os dados da amostra de entrada são considerados os neurônios da camada de entrada, enquanto a última camada da rede é chamada de camada de saída.
Nesse caso, a rede aprende a aplicar uma hierarquia de transformações lineares ou não lineares (através das ativações) gerando novas representações do dado de entrada, para que seja possível, por exemplo, realizar
classificações.
Esse modelo é chamado Perceptron de Múltiplas Camadas, ou MLP (Multilayer Perceptron).
Uma rede neural é considerada profunda quando ela possui mais de duas camadas escondidas.
O algoritmo que permite o aprendizado da rede neural é chamado de retropropagação(backpropagation).
Basicamente o que se chama de “aprendizado” em redes neurais é o ajuste nos pesos (w) e biases (b) dos neurônios para aproximar a saída da rede de uma função y(x) para toda entrada de treinamento x.
Para medir o quão próximo a rede está do objetivo, são utilizadas funções de custo (também chamadas de funções de perda).
Por exemplo, a função de custo quadrático é comumente utilizada em problemas de regressão.
Σ i (yi – Ŷi)2
Onde yi é a saída do nó e o Ŷi é a saída desejada, então, quanto menor a diferença entre eles, mais próximo de zero, e é exatamente o que se quer para minimizar a perda.
Em resumo, quanto mais próximo de zero, menor o custo, melhor o desempenho da rede.
Quando falamos em custo, podemos pensar em erro da rede, quanto maior o custo, mais a rede tá errando.
Detalhes
O elevado ao quadrado na fórmula, é para garantir que a saída vai ser sempre positiva.
O somatório, é porque são vários neurônios, vários nós da rede.
Outro detalhe é que o Y não necessariamente tem que ser um número, ele pode ser um vetor, uma matriz representando uma imagem por exemplo.
Funções de ativação
As funções de ativação introduzem um componente não linear nas redes neurais, de forma a possibilitar que elas absorvam informações não apenas em relações lineares entre as variáveis dependentes e independentes.
As funções de ativação são fundamentais para que nossas redes neurais funcionem em tarefas como traduções de idiomas (Processamento de Linguagem Natural), classificações de imagens (Visão Computacional), etc.
Só com transformações lineares, nunca seríamos capazes de executar tais tarefas.
Algumas das funções mais utilizadas são: Sigmóide, Tanh, ReLU, Leaky ReLU, Softmax…
Backpropagation
O algoritmo que possibilita o aprendizado da rede neural é chamado de retropropagação (backpropagation).
O backpropagation utilizam a descida do gradiente para ajustar os parâmetros das redes.
A descida do gradiente é um método utilizado na otimização, para encontrar um mínimo (local) de uma função.
O que entendemos como aprendizado em redes neurais, é o ajuste nos pesos(w) e viés ou em inglês, biases(b) dos neurônios para aproximar a saída da rede de uma função y(x) para toda entrada de treinamento x.
Uma rede neural não tem uma memória de eventos onde vai guardando todo um histórico de ações e suas recompensas.
O que ela tem é uma tabela com as probabilidades de cada ação e suas recompensas em um determinado estado.
Então, o que ela faz é: a cada ação ela vê, aqui tive uma resposta positiva, aqui negativa, aqui muito positiva, aqui muito negativa.
E a cada ação, ela atualiza a tabela.
Ou seja, a cada momento ela olha só o passo anterior, a tabela com os estados das respostas mostrando o quanto ela está próxima da resposta correta.
Daí ela vai testando e alterando os pesos pra tentar conseguir respostas que tragam uma recompensa maior, isto é, respostas mais acertivas no geral.
Esse processo se chama retropropagação.
Basicamente, o algoritmo de retropropagação altera os valores dos pesos e bias da rede otimizando a função de custo.
Ele volta nas camadas da rede para atualizar os pesos e recompensas da tabela de estado, baseado na função de custo.
Sigmoide
A função logística ou sigmoide produz valores no intervalo [0, 1].

Sua maior vantagem é que o valor da derivada é máximo quando x está próximo de 0, o que tende a levar o resultado para as extremidades do intervalo [0, 1] ao longo do treinamento, o que é desejável em problemas de classificação por exemplo.
Mas, sua característica não-linear, aumenta o custo computacional.
Além disso, a função sigmoide não é centrada em zero.
Ela ainda apresenta platôs para valores de x muito altos ou muito baixos, o que faz com que a derivada nessas regiões se aproxime de zero.
A soma dessas características não faz da função sigmoide uma boa opção para ativação das camadas escondidas.
A função sigmoide é útil na camada de saída, para produzir probabilidades em problemas de classificação binária, já que seus resultados, na faixa de [0, 1], podem ser interpretados como a probabilidade de determinada objeto ser ou não de determinada classe.
Softmax
Softmax é uma generalização da função sigmoide para casos não-binários.
Ela não costuma ser aplicada às camadas escondidas da rede neural, mas sim na camada de saída de problemas de classificação multiclasse.
Em um problema com 3 classes, por exemplo, a função softmax vai produzir 3 valores, que somam 1, onde cada valor representa a probabilidade da instância pertencer a uma das 3 possíveis classes.
Implementando um MLP
O código cria um pequeno dataset com pontos distribuídos de forma circular usando a biblioteca scikitlearn.
O dataset é composto por pontos de duas dimensões (duas features) que pertencem a dois conjuntos de classe, vermelho(0) e azul(1).
o scikit-learn inclui vários geradores de amostra aleatória que podem ser usados para construir conjuntos de dados artificiais de tamanho e complexidade controlados.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets
#Setando o seed para gerar uma sequencia conhecida
tf.random.set_seed(0)
np.random.seed(0)
#gerando o dataset
dataset_X , dataset_Y = sklearn.datasets.make_circles(n_samples=100, shuffle=True, noise=0.05, random_state=100, factor=0.8)
#plotando o dataset
plt.scatter(dataset_X[:,0], dataset_X[:,1], s=40, c=dataset_Y ,
cmap=plt.cm.Spectral)
n_samples
O n_samples é um int ou tupla de dois elementos, é opcional (padrão = 100), é o número total de pontos gerados.
Para números ímpares, o círculo interno terá um ponto a mais que o círculo externo.
Se for tupla de dois elementos, é o número de pontos no círculo externo e no círculo interno respectivamente.
shuffle
O shuffle, é um bool, é opcional (padrão = True), determina se deve embaralhar as amostras ou não.
noise
O noise é um double ou None (padrão = None), é o desvio padrão do ruído gaussiano adicionado aos dados.
random_state
O random_state é um int, uma instância de RandomState, (padrão = None).
Determina a geração de números aleatórios para embaralhamento e ruído do conjunto de dados.
Passa um int para saída reproduzível em várias chamadas de função.
factor
O factor é um double que fica entre 0 < double < 1 (padrão = .8), é um fator de escala entre o círculo interno e o externo.
Na próxima aula, a gente vai construir um multilayer perceptron (MLP) para utilizar com esses dados.