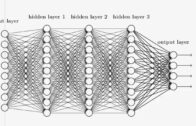
Aula 03 – Tensor Flow – Redes Neurais no Colab
Aula 03 – Tensor Flow – Redes Neurais no Colab
Voltar para página principal do blog
Todas as aulas desse curso
Aula 02 Aula 04
Meu github:
https://github.com/toticavalcanti
Documentação oficial do TensorFlow:
https://www.tensorflow.org/
Link para o notebook da aula:
notebook-da-aula

Python com Tensorflow
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Link do código fluente no Pinterest
Aproveito para deixar meus link de afiliados:
Hostinger
Digital Ocean
One.com
Aula 03 – Tensor Flow – Redes Neurais no Colab
Para aula prática, vamos utilizar o google colab.
Continuação do código
build_net()
A função build_net() recebe como parâmetro a quantidade de features e classes usadas no problema.
Nesse caso, tanto a quantidade de features quanto a de classes são iguais a 2.
def build_net(n_features , n_classes):
# Placeholders
# shape=[None] indica que o batch pode ser de qualquer tamanho
X_placeholder = tf.placeholder(dtype=tf.float32 , shape=[None , n_features])
Y_placeholder = tf.placeholder(dtype=tf.int64 , shape=[None])
# X_placeholder é camada de entrada da rede
# Y_placeholder é o vetor que contém os labels do dataset
# eles serão utilizados para comparação com a saída da rede.
#camada oculta
#O segundo argumento (100) é o número de neurônios / nós da camada.
layer1 = tf.layers.dense(X_placeholder , 100, activation=tf.nn.relu)
#camada de saída
out = tf.layers.dense(layer1 , n_classes , name="output")
#adaptando o vetor Y para o modelo One−Hot Label
one_hot = tf.one_hot(Y_placeholder , depth=n_classes)
# O vetor de labels, o Y_placeholder, é convertido para o formato OneHot
# (por exemplo, a label 0 se torna o vetor [1,0] e o label 1 se torna
# o vetor [0,1]), dessa forma é possível a comparação com a saída da rede.
#função de perda/custo/erro
loss = tf.losses.softmax_cross_entropy(onehot_labels=one_hot , logits=out)
# a função Entropia Cruzada é usada em conjunto com uma camada softmax
# logits são os valores a serem usados como entrada para softmax
# Logit é uma função que mapeia probabilidades [0, 1]para [-inf, +inf].
# Softmax é uma função que mapeia [-inf, +inf] para [0, 1] semelhante à sigmóide.
# Estamos aplicando a função softmax aos números logit para normalizá-los.
#otimizador
opt = tf.train.GradientDescentOptimizer(learning_rate =0.07). minimize(loss)
# quanto menor o learning_rate mais demorado
#classe do exemplo
softmax = tf.nn.softmax(out)
class_ = tf.argmax(softmax, 1)
# tensores que classificam um exemplo de entrada da rede
# argmax retorna o índice com o maior valor entre os eixos de um tensor
# Acurácia
compare_prediction = tf.equal(class_ , Y_placeholder)
# equal retorna o valor true de (x == y).
accuracy = tf.reduce_mean(tf.cast(compare_prediction , tf.float32))
# reduce_mean calcula a média dos elementos nas dimensões de um tensor.
return X_placeholder , Y_placeholder , loss , opt, class_ , accuracy
# tensores que calculam a acurácia da rede
Em seguida a sessão é iniciada, ela obtém o número de features e carrega o modelo.
#iniciando a sessão
sess = tf.InteractiveSession()
#numero de classes do problema
num_classes = 2
#obtendo o número de features
n_features = dataset_X.shape[1]
#carregando o modelo
X_placeholder , Y_placeholder , loss , opt, class_ , accuracy = build_net(n_features ,num_classes)
#inicializando as variáveis
sess.run(tf.global_variables_initializer())
draw_separator
Função que desenha o separador das classes
def draw_separator(X, Y, sess, X_placeholder, class_):
x_min, x_max = X[:, 0].min() - 0.3 , X[:, 0].max() + 0.3
y_min, y_max = X[:, 1].min() - 0.3 , X[:, 1].max() + 0.3
h = 0.01
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# class_ são as classes retornadas pela argmax
Z = sess.run(class_, feed_dict={X_placeholder:np.c_[xx.ravel(), yy.ravel()] })
# Coloca o resultado em um gráfico de cores
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.axis('on')
# Plota também os pontos de treinamento
plt.scatter(X[:, 0], X[:, 1], s=40, c=Y, cmap=plt.cm.Spectral)
Número de épocas
O código a seguir define o número de épocas no treinamento da rede, um laço executa o treinamento da rede mil vezes (mil épocas) usando todo o dataset.
Obs.
Como o tamanho do dataset, neste exemplo, é pequeno, o método de dividir o dataset em lotes não é usado.
#definindo o numero de épocas
epochs = 1000
for i in range(epochs):
#treinamento (OBS: mini−batch não usado por causa do tamanho pequeno do dataset)
sess.run(opt, feed_dict={X_placeholder: dataset_X , Y_placeholder: dataset_Y})
#a cada 100 épocas o erro é impresso
if i % 100 == 0:
erro_train = sess.run(loss , feed_dict={X_placeholder: dataset_X, Y_placeholder: dataset_Y})
print("O erro na epoca", i,":", erro_train)
# calculando a acurácia
acc = sess.run(accuracy , feed_dict={X_placeholder: dataset_X, Y_placeholder: dataset_Y})
print("accuracia do modelo:", acc)
# O feed_dict define um valor para o tensor
cla = sess.run(class_ , feed_dict={X_placeholder: dataset_X[:1]})
print("a classe do ponto", dataset_X[:1], "e:", cla)
# desenhando o separador
draw_separator(dataset_X , dataset_Y , sess , X_placeholder , class_)