Aula 04 – Complexidade de Fibonacci com Programação Dinâmica

toticavalcanti

Aula 04 – Complexidade de Algoritmo

Fibonacci com Programação Dinâmica

Reduzindo a complexidade da função fibonacci recursiva para O(n).

Será utilizada a técnica de programação dinâmica.

Fibonacci com Programação Dinâmica

Voltar para página principal do blog

Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook

Esse é o link do código fluente no Pinterest

Meus links de afiliados:

Meu github:
https://github.com/toticavalcanti

Programação Dinâmica

Seu criador Richard Bellman explica o raciocínio por trás do termo programação dinâmica em sua autobiografia, Eye of the Hurricane: Uma Autobiografia (1984).

Ele explica que trabalhava na RAND (research and development) nos anos 50.

O secretário de defesa na época era Charles Erwin Wilson, e ele não gostava do termo pesquisa, na sua autobiografia ele diz:

“ele tinha um medo patológico e ódio da palavra pesquisa, não estou usando o termo de ânimo leve, eu estou usando isso precisamente, o rosto se encheria, ele ficaria vermelho, e ele ficaria violento se as pessoas usassem o termo pesquisa em sua presença.”

Por isso ele diz também: “Os anos 50 não foram bons anos para matemática”.

A primeira tarefa de Bellman foi encontrar um nome para processos de decisão em múltiplos estágios, que soassem bem aos ouvidos de Wilson.

Pensou em várias palavras e acabou chegando ao termo programação dinâmica, pois achou que o termo dinâmico tem uma propriedade muito interessante como um adjetivo, e é impossível usar a palavra dinâmica em um sentido pejorativo.

Aplicando a técnica

Aplicaremos a técnica de programação dinâmica para reduzir a complexidade da função de fibonacci recursiva de O(2^n), para O(n).

Programação dinâmica

Programação dinâmica é um método de construção de algoritmos, geralmente para solução de problemas computacionais de otimização combinatória.

A programação dinâmica é principalmente uma otimização sobre a recursão simples.

Onde quer que vejamos uma solução recursiva que tenha chamadas repetidas para as mesmas entradas, podemos otimizá-la usando a Programação Dinâmica.

A ideia é simplesmente armazenar os resultados dos subproblemas, para que não tenhamos que recalculá-los quando for necessário posteriormente.

Essa otimização simples reduz as complexidades de tempo de exponencial para polinomial.

É isso que vamos fazer agora.

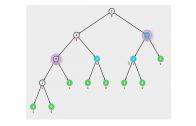
Veja no grafo abaixo que a função de fibonacci recursiva simples, que vimo aula passada, faz recálculos desnecessários.

Ela sabe que o fib(0) é 0(zero) e que fib(1) é 1, não precisa calcular, o fib(2) ela vai calcular somando 0(n – 2) com 1 (n – 1), então fib(2) é 1, só que ela faz isso 3 vezes, mas bastava fazer uma vez e memorizar que fib(2) é 1.

A mesma coisa acontece com fib(3), que é calculado duas vezes.

Com a programação dinâmica aplicada a esse caso, evitaremos esses recálculos desnecessários.

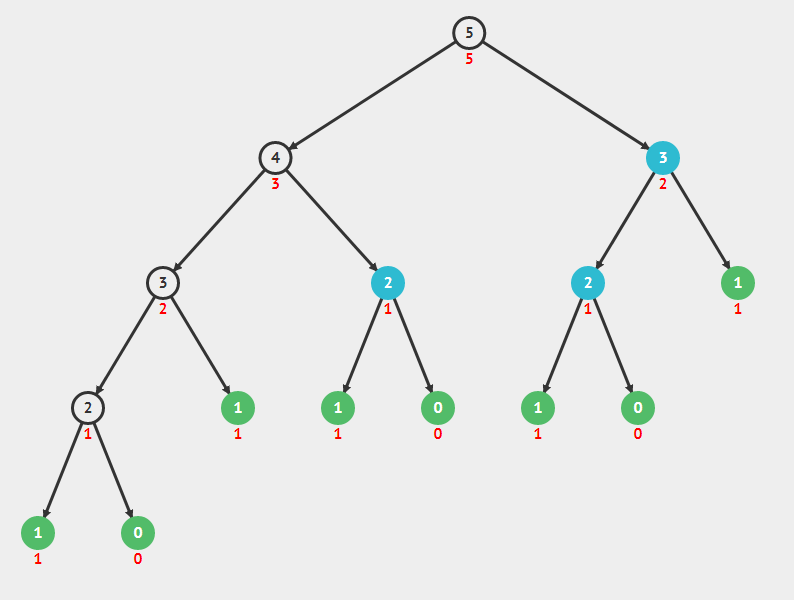
Gráfico das chamadas recursivas da função fibo()

O código a seguir é exatamente o mesmo da aula passada, mas, coloquei algumas instruções a mais(em azul), apenas para medir o tempo de execução do código e comparar as duas implementações:

Fibonnaci com complexidade de O(2^n) (código da aula passada):


import time
#Recursiva, complexidade O(2^n)

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n - 1) + fib(n - 2)

def main():
    n = int(input())
    t0= time.process_time()
    print( fib(n) )
    t1 = time.process_time() - t0
    print("Time elapsed: ",abs(t1 - t0))
if __name__ == "__main__":
    main()

O arquivo texto de input(input.txt) tem o número 36, que nosso algoritmo deve dá como resposta 14930352.

Vamos medir a execução e ver quanto tempo ele gasta.

Saída:

14930352
Time elapsed: 8.15625

Agora a implementação da Fibonnaci recursiva, com programação dinâmica, onde os resultados das computações são guardados, para evitar recálculos:

Fibonnaci com complexidade de O(n) (código dessa aula):


import time
#Recursiva, complexidade O(n) com memorização (programação dinâmica)
def fib(n, computed = {0: 0, 1: 1}):
    if n not in computed:
        computed[n] = fib(n - 1, computed) + fib(n - 2, computed)
    return computed[n]

def main():
    n = int(input())
    t0= time.process_time()
    print( fib(n) )
    t1 = time.process_time() - t0
    print("Time elapsed: ",abs(t1 - t0))

if __name__ == "__main__":
    main()

Saída:

14930352
Time elapsed: 0.03125