Aula 08 – Scikit-Learn – Support Vector Machine ou máquina de vetores de suporte
Scikit-Learn – Support Vector Machine ou máquina de vetores de suporte
Máquina de vetores de suporte ou SVM
Voltar para página principal do blog
Todas as aulas desse curso
Aula 07 Aula 09
Link do meu Github com o script dessa aula:
Download do script da aula
Link da documentação oficial do Sklearn:
https://scikit-learn.org/stable/

máquina de vetores de suporte (SVM)
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
Nessa aula iremos aprender sobre como o SVM funciona
SVM ou Support Vector Machine
SVM ou Support Vector Machine é um algoritmo de aprendizado de máquina supervisionado que pode ser usado para desafios de classificação ou regressão.
Aplica-se na resolução de problemas lineares e não lineares, funciona bem para muitos problemas práticos.
A ideia do SVM é simples: o algoritmo cria uma linha ou um hiperplano que separa os dados em classes.
Teoria
Na primeira aproximação, o que os SVMs fazem é encontrar uma linha de separação (ou hiperplano) entre as classes.
O SVM é um algoritmo que pega os dados como uma entrada e gera uma linha que separa essas classes, se possível.
Vamos começar com um problema. Suponha que você tenha um conjunto de dados, conforme mostrado abaixo, e precise classificar os retângulos verdes e bolas vermelhas.
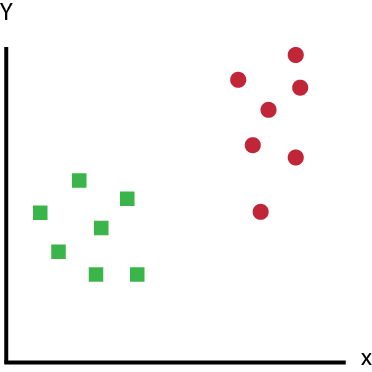
Qual o hiperplano que diferencia muito bem as duas classes?
A tarefa é encontrar uma linha ideal que separe esse conjunto de dados em duas classes (digamos verde e vermelho).
Mas, como você percebe, não há uma linha exclusiva que faça o trabalho.
Na verdade, temos infinitas linhas que podem separar essas duas classes.
Então, como o SVM encontra o ideal ???
Vamos pegar alguns candidatos prováveis e descobrir por nós mesmos.
Temos dois candidatos aqui, o hiperplano A e o B.
Qual das opções de acordo com você melhor separa os dados?
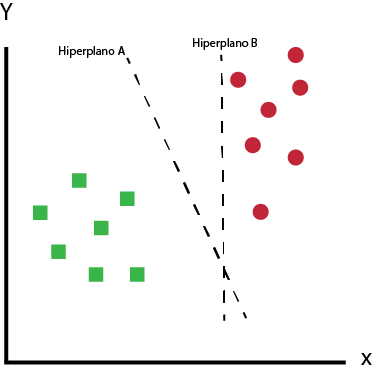
Qual das opções de acordo com você melhor separa os dados?
Se você acha que é o hiperplano A, então parabéns, essa é a linha que estamos procurando.
Intuitivamente é fácil perceber que o hiperplano A é quem melhor classifica o conjunto de dados.
O hiperplano B na imagem acima está bem próximo da classe vermelha.
Embora o B classifique esse conjunto de dados, esse hiperplano não é generalista, e no aprendizado de máquina, o objetivo é obter um separador mais generalista.
Como o SVM encontra o melhor hiperplano?
O SVM encontra os pontos mais próximos de ambas as classes nesse caso, já que são apenas duas.
Esses pontos são chamados vetores de suporte.
Agora, calculamos a distância entre a linha e os vetores de suporte.
Essa distância é chamada de margem.
Nosso objetivo é maximizar a margem.
O hiperplano para o qual a margem é máxima é o hiperplano ideal.
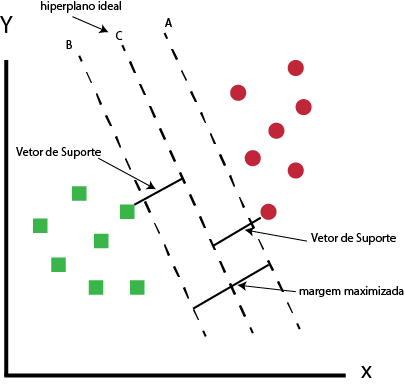
Hiperplano ótimo usando o algoritmo SVM
Assim, o SVM tenta estabelecer um limite de decisão de tal maneira que a separação entre as duas classes seja tão ampla quanto possível.
Tarefa
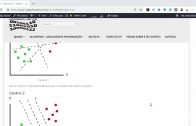
Identificar qual dos três hiperplanos (A, B e C) é o melhor hiperplano para classificar quadrados verdes e círculo vermelhos?
Cenário 1
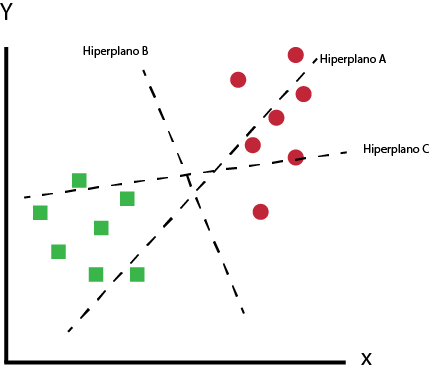
Cenário 1
Nesse cenário, o hiperplano B executou o trabalho da melhor maneira.
Cenário 2
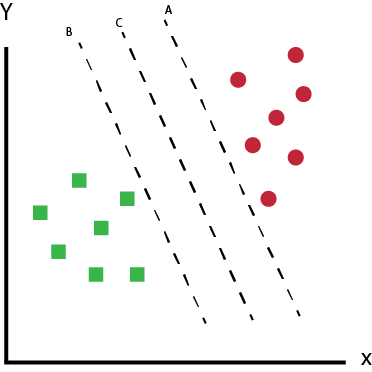
Cenário 2
Tarefa
Identificar qual dos três hiperplanos (A, B e C) é o melhor hiperplano para classificar quadrados verdes e círculo vermelhos?
Aqui todos estão segregando bem as classes. Então, como podemos identificar o melhor hiperplano?
Aqui, maximizar as distâncias entre o ponto de dados mais próximo (de qualquer classe) e o hiperplano nos ajudará a decidir qual o melhor hiperplano.
Essa distância é chamada de Margem. Veja a figura abaixo:
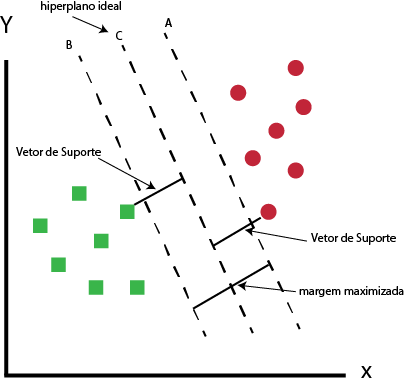
Maximizar a margem
Na figura acima, você pode ver que a margem para o hiperplano C é alta quando comparada a ambos, A e B.
Então nomeamos o melhor hiperplano como C.
O motivo de selecionar o melhor hiper-plano, isto é, de margem máxima, é a robustez, se selecionarmos um hiperplano com margem baixa, haverá uma alta chance de falta de classificação.
Cenário 3
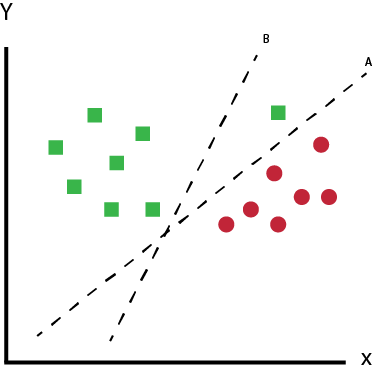
Cenário 3
Tarefa
Identificar o melhor hiperplano.
Vocês podem ter pensado no hiperplano B, já que ele tem uma margem maior em comparação a A.
Mas, aqui está o problema, o SVM seleciona primeiro o hiperplano que classifica as classes com precisão antes de maximizar a margem.
Aqui, o hiperplano B tem um erro de classificação e A classificou tudo corretamente.
Portanto, o melhor hiperplano é o A.
Cenário 4
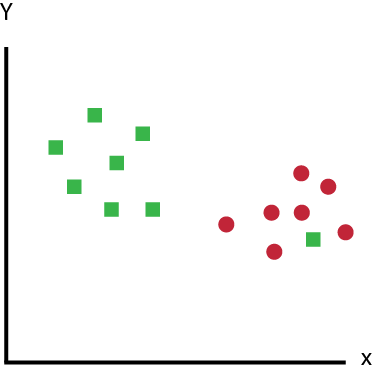
Cenário 4
Nesse caso, não consiguiremos separar as duas classes usando uma linha reta, pois um dos quadrados verdes está no território da classe (circular vermelha), trata-se de um outlier (ponto fora da curva).
O SVM tem um recurso para ignorar valores discrepantes, fora da curva e encontrar o hiperplano que tem margem máxima.
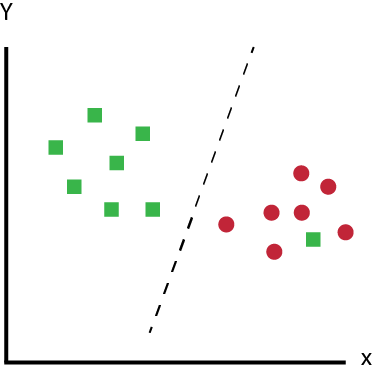
SVM é robusto para outliers
Portanto, podemos dizer que SVM é robusto para outliers.
Cenário 5
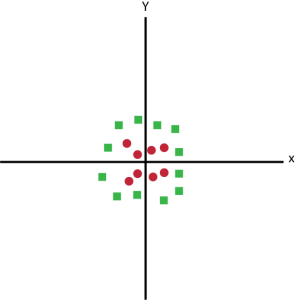
Cenário 5
No cenário 5, não podemos ter um hiperplano linear entre as duas classes, então como o SVM classifica essas duas classes?
Até agora, só olhamos para o hiperplano linear.
O SVM pode resolver esse problema facilmente!
Ele resolve esse problema introduzindo um recurso adicional.
Aqui, vamos adicionar um novo recurso z = x ^ 2 + y ^ 2.
Agora, vamos plotar os pontos de dados no eixo x e z:
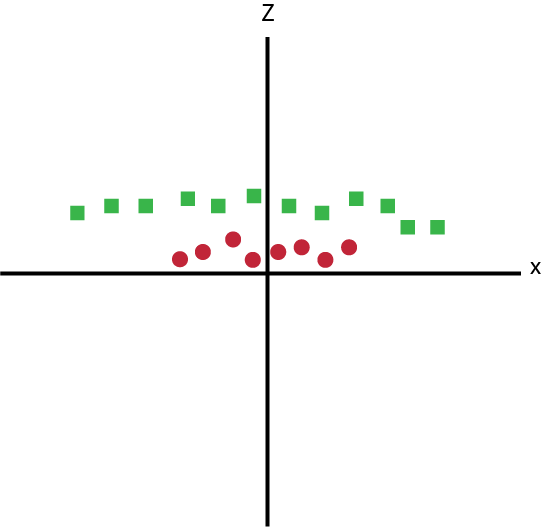
Pontos de dados no eixo x e z
No gráfico acima, os pontos a serem considerados são:
- Todos os valores para z são positivos sempre porque z é a soma quadrática de x e y.
- No gráfico original, os círculos vermelhos aparecem próximos da origem dos eixos x e y, levando a um valor menor de z e quadrados verdes relativamente longe da origem para um valor maior de z.
No SVM, é fácil ter um hiperplano linear entre essas duas classes.
Mas, outra pergunta urgente que surge é, devemos adicionar esse recurso manualmente para ter um hiperplano?
Não, o SVM tem uma técnica chamada truque do kernel .
Estas são funções que ocupam um espaço de entrada dimensional baixo e o transformam em um espaço dimensional mais alto, isto é, ele converte um problema não separável em um problema separável, essas funções são chamadas de núcleos (kernels).
É principalmente útil no problema de separação não linear.
Ele faz algumas transformações nos dados extremamente complexas e, em seguida, descobre o processo para separar os dados com base nos rótulos ou saídas que você definiu.
Quando olhamos para o hiperplano no espaço de entrada original, parece um círculo:

Espaço de entrada original
Na próxima aula vamos aplicar o algoritmo SVM ao Digits Dataset.
Nesse caso do digits dataset, teremos dez classes, veja como seria mais ou menos a representação dos hiperplanos.
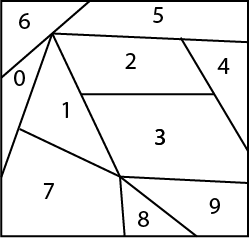
Hiperplano digits dataset
Como a gente define os parâmetros do SVM?
O valor dos parâmetros para algoritmos de aprendizado de máquina, melhora o desempenho do modelo.
Lista de parâmetros disponíveis no SVM:
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma=0.0, coef0=0.0,
shrinking=True, probability=False,tol=0.001, cache_size=200,
class_weight=None, verbose=False, max_iter=-1, random_state=None)
Vamos falar apenas sobre alguns parâmetros, os mais importantes e que impactam no desempenho do modelo: kernel, gamma, C e degree.
Obs. Exemplos aplicado ao iris dataset.
kernel
O kernel seleciona o tipo de hiperplano usado para separar os dados. O “linear” usará um hiperplano linear (uma linha no caso de dados 2D). ‘Rbf‘ e ‘poly‘ usam um hiperplano não linear. o valor padrão é “rbf“.
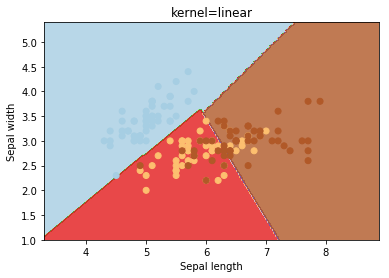
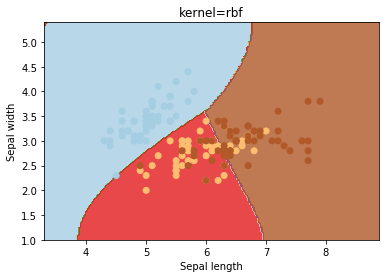
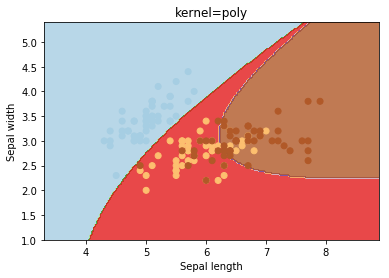
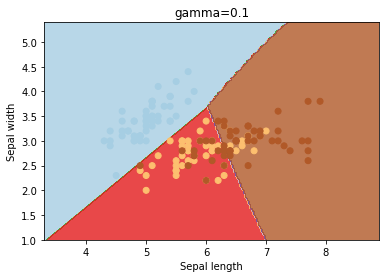
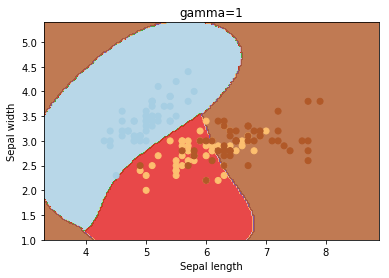
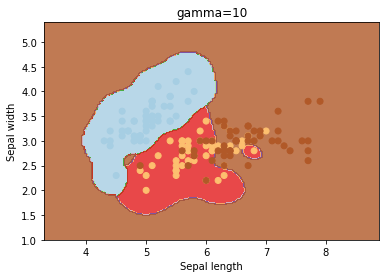
gamma
gama é um parâmetro para hiperplanos não lineares. Quanto maior o valor de gama, mais ele tenta ajustar-se exatamente ao conjunto de dados de treinamento.
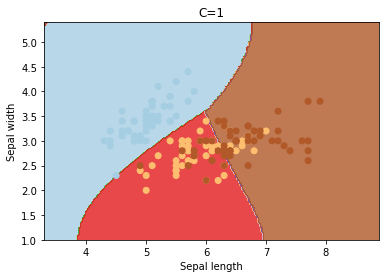
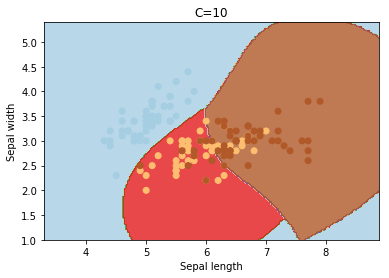
C
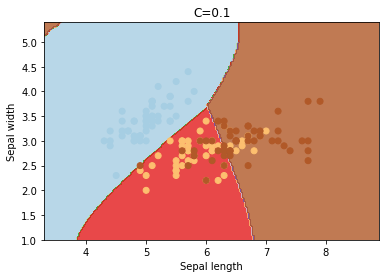
C é o parâmetro de penalidade do termo de erro. Ele controla o trade off entre o limite de decisão suave e a classificação correta dos pontos de treinamento. O aumento dos valores de C pode levar a um overfitting dos dados de treinamento.
degree
degree é um parâmetro usado quando o kernel é definido como “poly“. Basicamente, é o grau do polinômio usado para encontrar o hiperplano para dividir os dados.
Código para realizar as experiências acima, façam testes, mudem os parâmetros do kernel, gamma, C e degree.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# importar os dados do iris dataset
iris = datasets.load_iris()
X = iris.data[:, :2] # Nós só pegamos os dois primeiros recursos. Poderíamos
# evitar esse corte feio usando um conjunto de dados bidimensional
y = iris.target
# Criamos uma instância do SVM e ajustamos os dados. Nós não dimensionamos nosso
# dados já que queremos traçar os vetores de suporte
C = 1.0 # Parâmetro de regularização do SVM
svc = svm.SVC(kernel='rbf', C=1,gamma=0.5).fit(X, y)
# Cria uma malha para traçar o gráfico
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
plt.subplot(1, 1, 1)
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
Agora mostrar o gráfico:
plt.show()