Aula 08 – Tensor Flow – Redes Neurais – Classificação
Aula 08 – Tensor Flow – Redes Neurais – Classificação
Voltar para página principal do blog
Todas as aulas desse curso
Aula 07 Aula 09
Meu github:
https://github.com/toticavalcanti
Documentação oficial do TensorFlow:
https://www.tensorflow.org/
Link para o notebook da aula:
notebook-da-aula

Python com Tensorflow
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Link do código fluente no Pinterest
Aproveito para deixar meus link de afiliados:
Hostinger
Digital Ocean
One.com
Toti:
https://www.youtube.com/channel/UCUEtjLuDpcOvR3mIUr-viOA
Backing track / Play-along:
https://www.youtube.com/channel/UCT3TryVMqTqYBjf5g5WAHfA
Código Fluente
https://www.youtube.com/channel/UCgn-O-88XBAwdG9gUWkkb0w
Putz!
https://www.youtube.com/channel/UCZXop2-CECwyFYmHbhnAkAw
Fiquem a vontade para me adicionar ao linkedin.
Aula 08 – Tensor Flow – Redes Neurais – Classificação
Vamos construir um classificador simples.
Vamos para o código 😉
import matplotlib.pyplot as plt
%matplotlib inline
Nessas duas linhas estamos importando a biblioteca matplotlib e apelidamos ela de plt.
Vamos usar ela para plotar gráficos.
A linha:%matplotlib inline
É para que a saída dos comandos de plotagem seja exibida em linha, ou seja, diretamente abaixo da célula de código que o produziu.
Os gráficos resultantes também serão armazenados no documento do notebook.
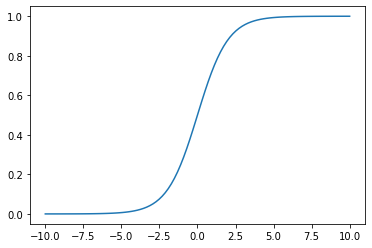
Depois temos a definição da função sigmoid(), a função de ativação:
def sigmoid(z):
return 1 / (1 + np.exp(-z))
Gerando os dados
sample_z = np.linspace(-10, 10, 100)
sample_a = sigmoid(sample_z)
A função linspace do numpy retorna números com espaçamento uniforme em um intervalo especificado.
Retorna números de amostras com espaçamento uniforme, calculados no intervalo [iniciar, parar].
No exemplo acima usamos numpy.linspace(start, stop, num=100)
Ou seja, vai gerar dados distribuídos de maneira uniforme, com 100 amostras variando entre -10 e 10.
O ponto final do intervalo pode ser opcionalmente excluído.
A linspace tem os seguintes parâmetros:
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
- start : array_like
O valor inicial da sequência. - stop : array_like
O valor final da sequência, a menos que o endpoint seja definido como False. Nesse caso, a sequência consiste em todas, exceto a última de num + 1 amostras uniformemente espaçadas, de modo que o ponto de parada é excluído. Observe que o tamanho da passo muda quando o endpoint é B. - num : int, opcional
Número de amostras a serem geradas. O padrão é 50. Não deve ser negativo. - endpoint : bool, opcional
Se for True, stop é a última amostra. Caso contrário, não está incluído. O padrão é True. - retstep : bool, opcional
Se for True, retorna (amostras, passo), onde passo é o espaçamento entre as amostras. - dtype : dtype, opcional
O tipo da matriz de saída. Se dtype não for fornecido, deduz o tipo de dados dos outros argumentos de entrada.
Função de ativação
Na linha seguinte: sample_a = sigmoid(sample_z) alimentamos a nossa função sigmoid com esses dados, isto é, os dados do sample_z.
Veja que a saída do gráfico plotado mostra que quanto maior o valor, mais a saída se aproxima de 1 e quanto menor o valor, mais a saída se aproxima de 0.
Sigmoid
Tecnicamente uma ativação é uma operação, então, vamos construir a operação Sigmoid, para isso vamos estender a classe Operation e implementar o método compute, que toda operação tem.
class Sigmoid(Operation):
def __init__(self, z):
super().__init__([z])
def compute(self, z_value):
return 1 / (1 + np.exp(-z_value))
Em seguida, vamos criar um conjunto de dados usando o sklearn.
from sklearn.datasets import make_blobs
O make_blobs() que vamos usar para gerar os dados tem os seguintes parâmetros:
sklearn.datasets.make_blobs(n_samples=100, n_features=2, *, centers=None, cluster_std=1.0, center_box=- 10.0, 10.0, shuffle=True, random_state=None, return_centers=False)
- n_samples : int ou array-like, default = 100
Se int, é o número total de pontos dividido igualmente entre os clusters.
Se for semelhante a uma matriz, cada elemento da sequência indica o número de amostras por cluster. - n_features : int, default = 2
O número de recursos para cada amostra. - center : int ou como um ndarray(n_centers, n_features), default = None
O número de centros a serem gerados ou as localizações dos centros fixos.
Se n_samples for um int e centers for None, 3 centros serão gerados
Se n_samples for semelhante a uma matriz, os centros devem ser None ou uma matriz de comprimento igual ao comprimento de n_samples. - cluster_std : float ou array-like, padrão = 1.0
O desvio padrão dos clusters. - center_box : tupla de float (min, max), default = (- 10,0, 10,0)
A caixa delimitadora para cada centro do cluster quando os centros são gerados aleatoriamente. - shuffle : bool, default=True
Mistura as amostras. - random_state : int, instância RandomState ou None, default = None
É usado para inicializar o gerador de número aleatório interno, determinando a geração desses números para a criação do conjunto de dados,
Passa um int para saída reproduzível em várias chamadas de função. - return_centers : bool, default = False
Se for Verdadeiro, então retorna os centros de cada cluster.
data = make_blobs(n_samples = 50, n_features = 2, centers = 2, random_state = 75, shuffle = False)
Então teremos 50 amostras de dados com duas features, isto é, duas variáveis independentes e também dois blobs, já que queremos simular uma classificação binária, tipo, pontos vermelhos e pontos azuis, bolinhas e quadrados, spam ou não spam, etc.
Execute:
dataA saída será algo como:
(array([[ 4.56366806, 2.38550006], [ 4.15165351, 5.79122957], [-1.12711589, 3.83230256], [-2.3718183 , 6.30442602], [-1.46281461, 8.15526926], [ 3.77803659, 3.45800335], [ 6.12000348, 3.18957996], [ 3.23678249, 4.21037718], [-0.68130304, 4.88173153], [-0.74959937, 4.52162834], [-1.90263115, 5.26659698], [ 5.0550793 , 2.23304562], [ 5.21188268, 3.69392105], [-0.63881764, 7.00942573], [ 4.6188071 , 2.89347134], [ 5.75599698, 2.38344229], [ 4.23428247, 2.89400059], [ 5.28254064, 4.03953668], [-0.65828004, 5.95264056], [ 5.38668626, 3.93807687], [ 6.22427149, 1.19775534], [ 5.60036085, 2.22050329], [-1.1788599 , 6.6069344 ], [ 0.08584655, 4.66018526], [ 6.51805758, 3.08666959], [ 4.07567013, 3.39923767], [ 0.7657604 , 5.5638716 ], [ 5.69629112, 3.7150426 ], [-0.5848107 , 5.25986698], [-0.45534906, 2.58849913], [-1.5137558 , 4.17878564], [-0.8715817 , 6.29487817], [ 4.97825983, 4.200051 ], [-1.56193838, 4.05477648], [-1.52492366, 5.49034698], [-0.52315441, 6.35414303], [ 4.39900896, 4.43338475], [ 5.1905785 , 3.46562862], [ 4.53966403, 2.03159979], [ 0.37734107, 5.61811114], [ 7.10213365, 4.39998422], [-1.83801655, 6.41619493], [-0.75060486, 6.53636014], [-1.04028059, 5.76802609], [ 5.15342914, 3.14265066], [-2.04173791, 4.8700765 ], [-1.2033877 , 6.85048961], [ 4.96900637, 2.80917048], [-0.46931407, 6.68625254], [ 4.41473358, 2.54240239]]), array([0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0]))
A primeira parte da saída, as tuplas com os números float são as features, as variáveis independentes.
A segunda parte da saída, o array, são os rótulos, os labels.
Veja qual o tipo de data
type(data)A saída será: tuple
Veja quem é o data[0] e quem é data[1]
data[0]Agora:
data[1]Vamos plotar um gráfico com esses dados
Começaremos separando as coisas.
features = data[0]
labels = data[1]
Estamos pegando todas as linhas só quem é da coluna 0 (zero) com features[:, 0] e todas as linhas só quem é da coluna 1 com features[:,1].
plt.scatter(features[:, 0], features[:,1])
A saída será algo como:
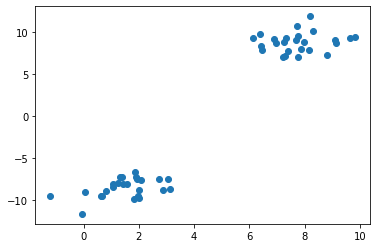
Scatter plot
É uma distribuição bem fácil para classificar, ela está bem separada.
O eixo x são as features 1, as da features[:, 0] e o eixo y as features 2, as da features[:, 1].
Vamos colocar cor para diferenciar as classes
plt.scatter(features[:, 0], features[:,1], c = labels)

Scatter plot com cor
Podemos usar também o cmap = ‘coolwarm’
plt.scatter(features[:, 0], features[:,1], c = labels, cmap = 'coolwarm')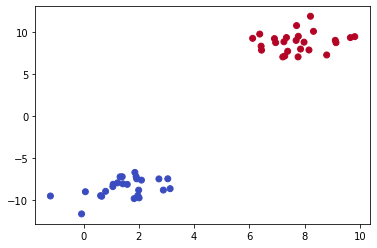
Scatter plot com cmap
Vamos primeiro construir manualmente uma linha que separe as duas classes.
x = np.linspace(-5, 10, 10)
y = - x + 3
plt.scatter(features[:, 0], features[:,1], c = labels, cmap = 'coolwarm')
plt.plot(x, y)
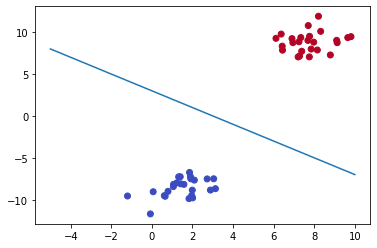
Scatter plot com linha de separação
Tudo abaixo da linha pertence a classe azul e tudo que tá acima da linha pertence a classe vermelha.
y = -mx + b
y = -1x + 3
Lembre-se que x e y são features, isto é, variáveis independentes.
feature2 = -1 * feature1 + 3
feature2 + feature1 – 3 = 0
Escrevendo em forma de matriz fica assim:
featureMatrix[1, 1] – 3 = 0
O que quer que seja a featureMatrix, todos os valores, features1 e features2 serão multiplicados por uma matriz comum de 1 por 1.
As features1 e features2 serão multiplicadas por um e subtraídas de -3, para resultar em zero.
Isso converte a linha em uma representação matricial, uma representação na forma de matriz, em que podemos inserir features nela.
Isso é bom porque a gente pode ter um placeholder pronto para alimentar essas features.
Equação da linha separadora: (1, 1) * f – 3 = 0
Equação do classificador
y = -x + 3
f1 = -f0 + 3
f1 + f0 – 3 = 0
(1,1) * F – 3 = 0
(1,1) é o Peso e 3 é um viés
Por exemplo, considere o ponto (8.0, 8.0)
res = np.array([1,1]).dot(np.array([[8.0],[8.0]])) - 3
print(res)
print(sigmoid(res))
Saída:
[13.]
[0.99999774]
13 > 0, o que implica, que ele pertence a classe vermelha
Por exemplo, considere o ponto (8.0, 8.0)
res2 = np.array([1, 1]).dot(np.array([[1], [-11.0]])) - 3
print(res2 )
print(sigmoid(res2))
Saída:
[-13.]
[2.2603243e-06]
Grafo
g = Graph()
g.set_as_default()
x = Placeholder()
w = Variable([1, 1])
b = Variable(-3)
z = add(matmul(w, x), b)
a = Sigmoid(z)
sess = Session()
sess.run(operation = a, feed_dict = {x: [8.0, 8.0]})
Saída:
array([0.99330715, 0.99330715])
O resultado são números bem próximos de 1.
sess.run(operation = a, feed_dict = {x: [1.0, -11.0]})
Saída:
array([1.19202922e-01, 8.31528028e-07])