Aula 09 – Scikit-Learn – Aplicando SVM ao Digits Dataset
Scikit-Learn – Aplicando SVM ao Digits Dataset
Aprendendo e prevendo com SVM
Voltar para página principal do blog
Todas as aulas desse curso
Aula 08 Aula 10
Link do meu Github com o script dessa aula:
Download do script da aula
Link da documentação oficial do Sklearn:
https://scikit-learn.org/stable/

Aplicando o SVM ao Digits Dataset
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
Antes de seguir
Vamos fazer uma breve análise das vantagens e desvantagens do SVM
Vantagens e desvantagens do SVM
- Vantagens:
- Funciona muito bem com margem de separação clara nos dados.
- É indicado para espaços dimensionais elevados, onde se tem muitas features.
- É muito bom em casos onde o número de features é maior que o número de amostras.
- Usa um subconjunto de pontos de treinamento na função de decisão (chamados de vetores de suporte), por isso, é eficiente em relação a memória.
- Desvantagens:
- Não funciona bem quando temos um grande conjunto de dados porque o tempo de treinamento necessário é maior.
- Também quando o conjunto de dados tem mais ruído, ou seja, onde as classes estão sobrepostas.
- O SVM não trabalha com probabilidade diretamente, elas são calculadas usando validação cruzada. É o método SVC da biblioteca scikit-learn do Python.
Nessa aula iremos aplicar o SVM ao Digits Dataset
Digits Dataset
Este conjunto de dados é composto por 1797 imagens 8×8, de dígitos manuscritos (0 à 9).
Exemplo:

Uma amostra de dígito
O conjunto de dados é um objeto semelhante a um dicionário que contém todos os dados e alguns metadados sobre os dados, como o dataset das iris das flores que já vimos nas aulas anteriores.
Os dígitos manuscritos são armazenados na chave .data, que é uma matriz n_samples e n_features.
No caso de problema supervisionado, uma ou mais variáveis de resposta são armazenadas na chave .target.
O digits.data, ou digits[‘data’], dá acesso aos recursos, isto é, as features que podem ser usadas para classificar as amostras de dígitos.
São 64 features em cada amostra, é uma matriz 8 x 8, e 8 * 8 = 64.
Cada feature das 64 que tem em cada amostra é um pixel da imagem, que pode tá totalmente sem cor (0), ou em graduações de cinza até o preto(255).
Diferente do iris dataset que tinha apenas 4 features que são os comprimentos das sépalas e pétalas e a largura das pétalas e sépalas, o digits dataset tem 64 features.
No iris dataset tínhamos nomes das features, porque fazia sentido, no digits dataset, os nomes das features são números, porque não faz sentido nomear pixels e sim numerá-los.
# importa os dataset que vem com o sklearn
from sklearn import datasets
#Carrega o digits dataset na variável digits
digits = datasets.load_digits()
#Mostra que há 1797 imagens (8 por 8 imagens para uma dimensionalidade de 64)
print("Forma de dados da imagem" , digits.data.shape)
#Mostra que há 1797 amostras (inteiros de 0 a 9)
print("Forma de dados do rótulo", digits.target.shape)
#Mostra os dados, as features de cada dígito manuscrito
digits.data
# Ou então
digits['data']
Saída:
array([[ 0., 0., 5., …, 0., 0., 0.],
[ 0., 0., 0., …, 10., 0., 0.],
[ 0., 0., 0., …, 16., 9., 0.],
…,
[ 0., 0., 1., …, 6., 0., 0.],
[ 0., 0., 2., …, 12., 0., 0.],
[ 0., 0., 10., …, 12., 1., 0.]])
E digits.target, ou digits[‘target’], fornece a resposta certa para cada dígito, ou seja, a classificação de cada dígito do conjunto de dados, o número correspondente a cada imagem de dígito que tentaremos fazer a máquina aprender a classificar.
digits.target
# Ou
digits['target']
Saída:
array([0, 1, 2, …, 8, 9, 8])
Forma dos vetores de dados
Os dados são representados em um array 2D, na forma (n_samples, n_features), embora os dados originais possam ter tido uma forma diferente.
Os dados desse conjunto digits dataset, já estão pré-processados, todas as amostras estão no mesmo formato matricial.
Na vida real os dados vem bruto, em um caso como esse dos dígitos manuscritos, podemos ter variações no formato matricial, variação nas resoluções, na forma como o dígito foi escaneado, etc.
Dados brutos normalmente precisam passar por um pré-processamento para deixar todas as amostras em uma mesma escala, todos em um mesmo formato e resolução.
No caso dos dígitos, os dados já estão todos no mesmo formato, escala, etc.
Cada amostra original é uma imagem de forma (8, 8) e pode ser acessada usando:
digits.images[0]
Saída:
array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
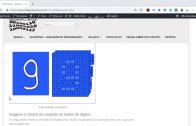
A imagem abaixo mostra mais ou menos como é essa representação matricial, no caso, em colorido( camadas red, green e blue).
Veja que a camada que está visível na figura, a camada red, está bem definida, com pixels cheios(255) e vazios(0), mostrando nitidamente que se trata de um dígito 9.

Propriedades dos dígitos
Imagens e rótulos do conjunto de dados de dígitos
O código abaixo mostra como são as imagens e os rótulos, visualizando os dados para ver com o que você está trabalhando.
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(20,4))
for index, (image, label) in enumerate(zip(digits.data[0:5], digits.target[0:5])):
plt.subplot(1, 5, index + 1)
plt.imshow(np.reshape(image, (8,8)), cmap=plt.cm.gray)
plt.title('Target: {}\n'.format(label, fontsize = 20))
Obs: A função zip(), pega as tuplas contendo a representação matricial dos primeiros 5 registros e o target, com a classificação do número.
Saída:
<matplotlib.axes._subplots.AxesSubplot object at 0x000002224FE3BD30>
<matplotlib.image.AxesImage object at 0x0000022252B8C978>
Text(0.5, 1.0, ‘Target: 0\n’)
<matplotlib.axes._subplots.AxesSubplot object at 0x000002225206A518>
<matplotlib.image.AxesImage object at 0x00000222523CB4A8>
Text(0.5, 1.0, ‘Target: 1\n’)
<matplotlib.axes._subplots.AxesSubplot object at 0x00000222523F2D68>
<matplotlib.image.AxesImage object at 0x00000222523B5CF8>
Text(0.5, 1.0, ‘Target: 2\n’)
<matplotlib.axes._subplots.AxesSubplot object at 0x000002225239D5F8>
<matplotlib.image.AxesImage object at 0x0000022252C23588>
Text(0.5, 1.0, ‘Target: 3\n’)
<matplotlib.axes._subplots.AxesSubplot object at 0x0000022252C56E48>
<matplotlib.image.AxesImage object at 0x0000022252BD1DD8>
Text(0.5, 1.0, ‘Target: 4\n’)
Para plotar a saída acima:
plt.show()Saída:
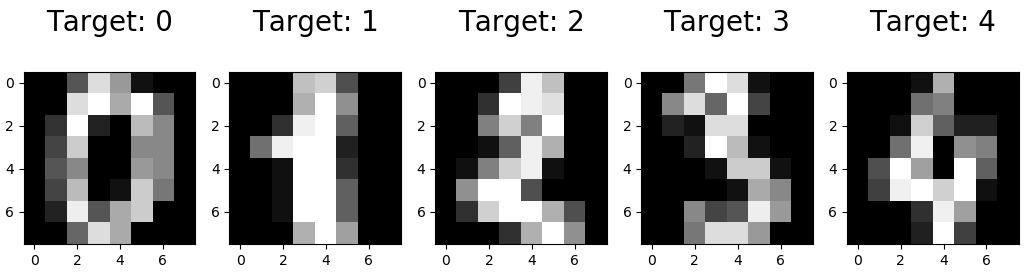
Visualizando Imagens e Labels no Digits Dataset
Aprendendo e prevendo
No caso do conjunto de dados de dígitos, a tarefa é prever, dada uma imagem, qual dígito ela representa.
Recebemos amostras de cada uma das 10 classes possíveis (os dígitos de zero a nove) nas quais nós ajustaremos um estimador para poder prever as classes às quais as novas amostras pertencem.
No scikit-learn, um estimador para classificação é um objeto Python que implementa os métodos fit(X, y) e predict(T).
Um exemplo de um estimador é a classe sklearn.svm.SVC, que implementa a classificação de vetor de suporte. O construtor do estimador usa como argumentos os parâmetros do modelo.
Por enquanto, vamos considerar o estimador como uma caixa preta:
#Importa o svm(support vector machine) do sklearn
from sklearn import svm
#Instancia um objeto svm em clf
clf = svm.SVC(gamma=0.001, C=100.)
Escolhendo os parâmetros do modelo
Neste exemplo, definimos o valor de gamma manualmente.
Para encontrar bons valores para esses parâmetros, podemos usar ferramentas como grid search e cross validation.
A instância do estimador clf (para classificador) é ajustada primeiro ao modelo, ou seja, deve aprender com o modelo.
Isso é feito passando nosso conjunto de treinamento para o método de ajuste (fit).
Para o conjunto de treinamento, usaremos todas as imagens do nosso conjunto de dados, exceto a última imagem, que reservaremos para a nossa previsão.
Selecionamos o conjunto de treinamento com a sintaxe Python [: -1], que produz uma nova matriz que contém todos os itens, exceto o último, de digits.data:
clf.fit(digits.data[:-1], digits.target[:-1])
Saída:
SVC(C=100.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=’ovr’, degree=3, gamma=0.001, kernel=’rbf’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Agora você pode prever novos valores.
Nesse caso, você irá usar a última imagem de digits.data.
Ao prever, você determinará a imagem do conjunto de treinamento que melhor corresponde à imagem.
clf.predict(digits.data[-1:])
Saída:
array([8])
A imagem correspondente é:

Como deu para notar, é uma tarefa desafiadora: afinal, as imagens são de baixa resolução.
Você concorda com o classificador?