Aula 13 – Curso de R – Funções Estatísticas e Geração de Sequências Randômicas
Aula 13 – Curso de programação em R
Funções Estatísticas e Geração de Sequências Randômicas

Funções Estatísticas e Geração de Sequências Randômicas
Página principal do blog
Todas as aulas desse curso
Aula 12 Aula 14
Antes, quero deixar meus links de afiliados pra vocês:
Hostinger
One.com
DigitalOcean
Se cadastrando, vocês poderão conhecer, usar e testar gratuitamente alguns recursos dos serviços oferecidos por eles.
Por favor, se gostarem do conteúdo dêem um joinha 👍, curtam e compartilhem a página do Código Fluente no Facebook.
Pinterest:
https://br.pinterest.com/codigofluente/
Endereço para baixar os arquivos e o script:
https://github.com/toticavalcanti/curso_r
Funções Estatísticas e Geração de Sequências Randômicas
| Lei | Função |
|---|---|
| Gaussian (normal) | rnorm(n, mean=0, sd=1) |
| exponential | rexp(n, rate=1) |
| gamma | rgamma(n, shape, scale=1) |
| Poisson | rpois(n, lambda) |
| Weibull | rweibull(n, shape, scale=1) |
| Cauchy | rcauchy(n, location=0, scale=1) |
| beta | rbeta(n, shape1, shape2) |
| ‘Student’ (t) | rt(n, df) |
| Fisher-Snedecor (F) | rf(n, df1, df2) |
| Pearson (x^2) | rchisq(n, df) |
| binomial | rbinom(n, size, prob) |
| multinomial | rmultinom(n, size, prob) |
| geometric | rgeom(n, prob) |
| hypergeometric | rhyper(nn, m, n, k) |
| logistic | rlogis(n, location=0, scale=1) |
| lognormal | rlnorm(n, meanlog=0, sdlog=1) |
| negative binomial | rnbinom(n, size, prob) |
| uniform | runif(n, min=0, max=1) |
| Wilcoxon’s statistics | rwilcox(nn, m, n), rsignrank(nn, n) |
Funções Estatísticas e Geração de Sequências Randômicas
Essas funções são úteis em estatísticas para gerar dados aleatórios, e no R, isso é muito usual em um grande número de funções de densidade de probabilidade.
Essas funções são da forma rfunc (n, p1, p2, …), onde func indica a probabilidade da distribuição, n o número de dados gerados, e p1, p2, …, são os valores dos parâmetros da distribuição.
A tabela acima fornece os detalhes de cada distribuição e os possíveis valores padrão (se nenhum valor padrão for indicado, isto significa que o parâmetro deve ser especificado pelo usuário).
A maioria dessas funções tem contrapartidas obtidas substituindo a letra r por d, p ou q para obter, respectivamente, a densidade de probabilidade (dfunc(x, …)), a densidade de probabilidade cumulativa (pfunc (x, …)) e o valor do quantil (qfunc (p, …), com 0 <p <1).
As duas últimas séries de funções podem ser usadas para encontrar valores críticos ou valores-P de testes estatísticos.
Esse post não é uma aula de estatística, mas, é importante falar sobre alguns conceitos estatísticos para entender melhor pelo menos algumas das funções da tabela acima (Funções Estatísticas e Geração de Sequências Randômicas), com isso agregamos conhecimento a nossa base de dados biológica.
😉
Nos exemplos iremos usar:
pnorm(), qnorm(), o pnormGC() do pacote tigerstats, para gerar uma vizualização gráfica e pchisq() para testar hipóteses.
Conceitos Estatísticos
Distribuição normal ou distribuição gaussiana
A distribuição normal também conhecida como gaussiana, é um lugar comum nas ciências naturais.
Sobre os eventos que seguem esse padrão, ou seja, esse comportamento, dizemos que eles seguem a distribuição normal, ou também, distribuição gaussiana, ou ainda, que seguem a curva de Gauss.
Frederick Gauss
No século XIX, Frederick Gauss, em seus estudos sobre comportamento padrão entre as amostras de eventos da natureza estudadas por ele, observou que grande parte desses eventos ficavam em torno de um valor médio, com uma certa variabilidade.
Um exemplo de distribuição gaussiana é a altura de uma determinada população.
Existem outras características físicas e sociais que tem um comportamento gaussiano.
Para determinar se uma variável aleatória específica segue uma distribuição normal, basta verificar se ela segue a função densidade de probabilidade, dada por:
A maior parte do que medimos é, de fato, a soma de muitas variáveis aleatórias randômicas (independent random variable – r.v.’s).
Por exemplo, você mede o comprimento de uma mesa com uma régua, o comprimento que você mede depende de muitos efeitos pequenos:
- paralaxe ótica, erro que ocorre pela observação errada na escala de graduação.
- calibração da régua,
- temperatura,
- sua mão trêmula, etc.
O que você mede não é apenas o que você pretende medir
Um medidor digital possui ruído eletrônico em vários locais em seu circuito.
Assim, o que você mede não é apenas o que você quer medir, mas adicionamos a ele um grande número de contribuições pequenas (ruídos).
Se este número de pequenas contribuições for grande, o Teorema do Limite Central (C.L.T.) afirma que a distribuição amostral das médias amostrais aproxima-se de uma distribuição normal à medida que o tamanho da amostra aumenta, não importa qual seja a forma da distribuição da população.
O C.L.T. nos diz que sua soma total é distribuída por Gauss.
Este é frequentemente o caso e é a razão pela qual as funções de resolução são geralmente gaussianas.
Nem todos os eventos aleatórios seguem Gauss
Existem outras distribuições além da distribuição de Gauss, como por exemplo:
- Distribuição de Poisson – comum na física quando se lida com processos de contagem
- Distribuição de Cauchy (também conhecida como Breit Wigner) – usada para descrever a forma dos espectros de radiação.
Se você observar a tabela Funções Estatísticas e Geração de Sequências Randômicas lá em cima, verá que o R fornece funcões para outras distribuições também, além de Gauss, que é a distribuição que iremos utilizar na prática aqui nessa aula.
Evento aleatório
Evento aleatório é a variável aleatória randômica que já falamos anteriormente, é algo que ocorre individualmente sem seguir regras ou padrões que pudessem nos possibilitar fazer previsões certeiras, como por exemplo, qual a face de um dado lançado cairá para cima.
Densidade de probabilidade
A função de densidade de probabilidade ajuda a identificar regiões de probabilidades superiores e inferiores para os valores de um evento aleatório.
A variável ou evento aleatório podem ser discretos ou contínuos.
- Contínuo – podem assumir valores que podem ser contados, ou seja, é um conjunto finito ou infinito contável, exemplo: o lançamento de uma moeda, ou de um dado.
- Discreto – podem assumir qualquer valor numérico em um determinado intervalo ou série de intervalos. É um conjunto infinito não enumerável. Podem assumir valores dentro de intervalos de números reais. Exemplo: o lançamento de martelo em competições esportivas é um exemplo de evento aleatório contínuo. Os valores do lançamento de um martelo atingem a distância máxima de 60 metros e a distância mínima classificatória de 30 metros.
Para um evento aleatório contínuo, a função usada para representar a distribuição de probabilidade é a função de densidade de probabilidade, ela descreve a forma da curva de distribuição da probabilidade de ocorrência de cada valor da variável aleatória contínua.
A probabilidade cumulativa determina a probabilidade de que uma observação aleatória extraída da população, seja menor ou igual a um determinado valor. Também é possível usar essas informações para determinar a probabilidade de que uma observação seja maior do que um determinado valor ou esteja entre dois valores.
Exemplo, os pesos de enchimento de latas de refrigerantes, seguem uma distribuição normal com uma média de 12 onças e um desvio padrão de 0,25 onças.
A densidade de probabilidade (FDP) descreve a probabilidade dos valores de peso de enchimento.
A probabilidade cumulativa (FDA) fornece a probabilidade acumulada para cada valor de x.
Quantil
Quantil são pontos estabelecidos em intervalos regulares a partir da função distribuição acumulada (FDA), de uma variável aleatória.
Os quantis dividem os dados ordenados em q subconjuntos de dados de dimensão essencialmente igual.
Exemplo, um quartil é qualquer um dos valores que dividem o conjunto ordenado de dados em quatro partes iguais, e assim cada parte representa 1/4 da amostra ou população.
Teste bicaudal (two-tailed)
Na estatística, um teste bicaudal (two-tailed), é um método no qual a área crítica de uma distribuição é bilateral.
Ela testa se uma amostra é maior ou menor que um determinado intervalo de valores.
As funções assumem a distribuição normal padrão μ (média) = 0 e σ² (desvio padrão^2) = 1
Obs. O desvio padrão é uma das medidas de variância mais utilizadas de um grupo de dados.
É usado em testes de hipóteses nulas e testes para significância estatística.
Vamos a um problema prático:
Esse exemplo a seguir encontra-se em:
https://www.inf.ufsc.br/~andre.zibetti/probabilidade/normal.html
Os dados de uma pesquisa mostram algumas informações sobre o tempo de cirurgias para recostrução em lesões do ligamento cruzado anterior ( ACL – Anterior Cruciate Ligament ), em hospitais com alto volume de cirurgia.
A partir dos dados foram calculados: o tempo médio de 129 minutos com um desvio padrão de 14 minutos.
Questões
- Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias, requerer um tempo maior do que dois desvios-padrão acima da média?
- Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias ser completada em menos de 100 minutos?
- Em qual tempo a probabilidade de uma cirurgia ACL em um hospital com alto volume de cirurgias é igual a 0.95?
Solução
Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias, requerer um tempo maior do que dois desvios-padrão acima da média?
1 − P(Z < 2) = 1 − ϕ(2) = 0.0228
1 - pnorm(2)
[1] 0.02275013Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias ser completada em menos de 100 minutos?
Seja X o tempo, onde X ∼ N(129, 14^2)
Z = (X − μ) / σ = (100 − 129) / 14
P(X < 100 ) = ϕ(−2.0714) = 0.01916072
pnorm(-2.0714)
[1] 0.01916072
Em qual tempo a probabilidade de uma cirurgia ACL em um hospital com alto volume de cirurgias é igual a 0.95?
z = qnorm(0.95) # fornece o valor de z para a probabilidade de 0.95
z
[1] 1.644854Outro exemplo
Encontre um número z positivo para que a área sob a curva normal padrão entre −z e z seja 0,95.
Aqui está a solução.
Se 95% da área estiver entre −z e z, então 5% da área deve ficar fora dessa faixa, como as curvas normais são simétricas, metade desse valor (2,5%) deve estar antes de –z e a outra depois de z.
Então a área sob a curva antes de z deve ser:
0.025 + 0.95 = 0.975
Portanto, o número z é, na verdade, o percentil 97.5 da distribuição normal padrão, e podemos encontrá-lo da seguinte maneira:
qnorm(0.025)
[1] -1.959964
qnorm(0.975)
[1] 1.959964
Veja que:
1 – 0.975 = 0.025
Ou
1 – 0.025 = 0.975
Então z é 1.959964, arredondando 1,96.
Gráficos
Podemos verificar este resultado graficamente usando o pnormGC(), para isso teremos que instalar alguns pacotes e dá um require no tigerstats:
install.packages("tigerstats")
install.packages("abd")
install.packages("mosaic")
install.packages("psych")
require(tigerstats)
pnormGC(c(-1.96,1.96),region="between",mean=0,
sd=1,graph=TRUE)Saída:
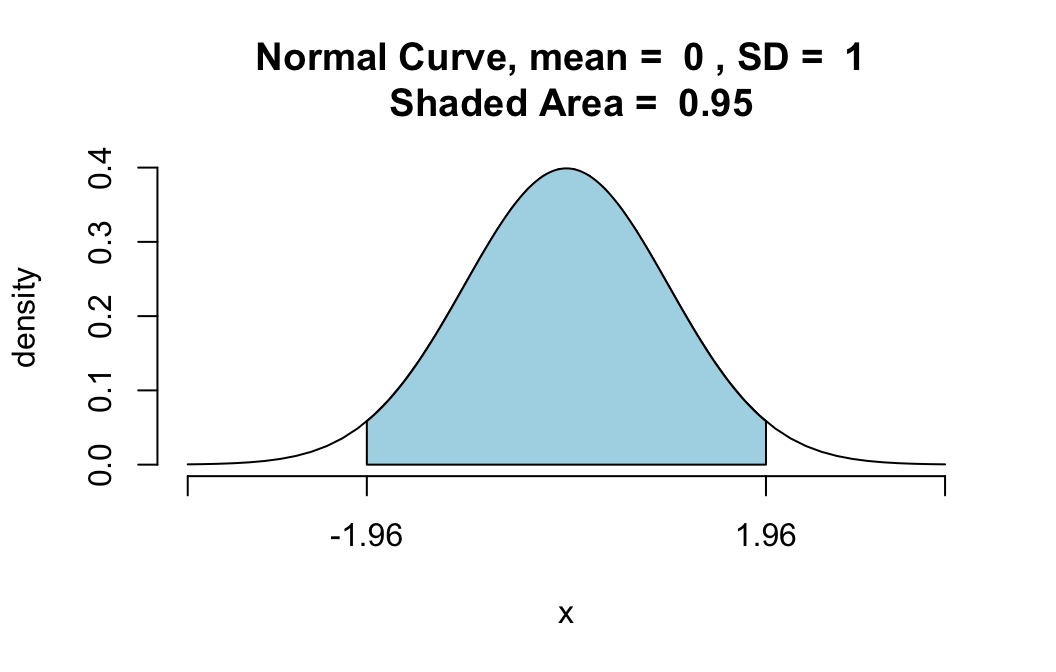
Valor da densidade da normal e da probabilidade no ponto -1.
dnorm(-1)
[1] 0.2419707
pnorm(-1)
[1] 0.1586553
Gera uma amostra de 10 elementos da normal padrão.
rnorm(10)
[1] -0.0442493 -0.3604689 0.2608995 -0.8503701 -0.1255832 0.4337861
[7] -1.0240673 -1.3205288 2.0273882 -1.7574165
O primeiro valor acima corresponde ao valor da densidade da normal:
densidade da normal
Com parâmetros
![]()
No ponto ![]()
O mesmo valor seria obtido substituindo ![]() por
por ![]() na expressão da normal padrão:
na expressão da normal padrão:
(1/sqrt(2*pi)) * exp((-1/2)*(-1)^2)
[1] 0.2419707
A função pnorm(-1) calcula a probabilidade ![]()
E o comando rnorm(10) gera uma amostra de 10 elementos da normal padrão.
Para a versão unicaudal (one-tailed) do mesmo teste, qnorm (0.05) ou 1 – qnorm (0,95) será usado dependendo da forma da hipótese alternativa.
Teste qui-quadrado
O valor P de um teste, digamos x^2 = 3.84 com df (Degrees of freedom) = 1, é:
1 - pchisq(3.84, 1)
[1] 0.05004352