Aula 17 – Tensor Flow – Redes Neurais – Rede Neural Convolucional
Aula 17 – Tensor Flow – Redes Neurais – Rede Neural Convolucional
Voltar para página principal do blog
Todas as aulas desse curso
Aula 16 Aula 18
Meu github:
https://github.com/toticavalcanti
Documentação oficial do TensorFlow:
https://www.tensorflow.org/
Quer aprender python3 de graça e com certificado? Acesse então:
https://workover.com.br/python-codigo-fluente

Python com Tensorflow
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
https://digitalinnovation.one/
Link do código fluente no Pinterest
Aproveito para deixar meus link de afiliados:
Hostinger
Digital Ocean
One.com
Toti:
https://www.youtube.com/channel/UCUEtjLuDpcOvR3mIUr-viOA
Backing track / Play-along:
https://www.youtube.com/channel/UCT3TryVMqTqYBjf5g5WAHfA
Código Fluente
https://www.youtube.com/channel/UCgn-O-88XBAwdG9gUWkkb0w
Putz!
https://www.youtube.com/channel/UCZXop2-CECwyFYmHbhnAkAw
Fiquem a vontade para me adicionar ao linkedin.
Aula 17 – Tensor Flow – Redes Neurais – Rede Neural Convolucional
Rede Neural Convolucional (CNN)
Uma Rede Neural Convolucional (ConvNet / Convolutional Neural Network / CNN) é uma rede neural artificial do tipo feed-forward.
As redes tem o nome de acordo com a forma como as informações fluem através de uma série de operações matemáticas feitas nos nós da rede.
As redes feed-forward permitem que os sinais viajem apenas em uma direção, da entrada para a saída.
As redes de feed-back, ou recorrentes, ou ainda interativas, são bidirecionais, ou seja, podem ter os sinais viajando em ambas as direções, introduzindo loops na rede.
Elas são legais porque tem estado, então por exemplo, a forma como uma rede feed-forward opera é assim, digamos que ela tá fazendo algum reconhecimento em tempo real em um vídeo.
Ela vai recebendo uma imagem após outra, só que ela não lembra de nada das imagens anteriores, ela não guarda as informações das imagens que passaram, porque ela não tem estado, ao contrário das recorrentes.
São interessantes quando temos estrutura temporal nos dados, mas é uma rede difícil de treinar e não é tão utilizada para coisas assim como processamento de imagens, áudios, enfim.
Backpropagation vs. rede neural feed-back
A retropropagação ou em inglês, backpropagation, é o algoritmo usado para encontrar pesos ótimos em uma rede neural por meio da descida de gradiente.
É chamado assim porque os derivados de erro são propagados de volta pela rede e os pesos são atualizados de acordo.
Uma rede neural recorrente (RNN) é um tipo de arquitetura de rede neural na qual existem neurônios na rede que têm pesos que se retroalimentam.
Dessa forma, temos um estado particular da rede em relação ao seu peso em cada ponto no tempo.
Isso permite a modelagem de dados temporais ou sequenciais, como dados de série temporal ou dados de vídeo.
Os RNNs podem ser treinados usando variantes da retropropagação, como retropropagação através do tempo (BPTT – Backpropagation Through Time).
No entanto, RNNs padrão, com neurônios recorrentes simples, normalmente sofrem do problema de desaparecimento de gradiente, uma vez que os derivados de erro não podem ser propagados de volta através da rede em cada etapa de tempo efetivamente sem primeiro morrer desaparecendo para zero ou explodindo para o infinito.
Assim, frequentemente outros tipos de neurônios (células) recorrentes são empregados em arquiteturas RNN para mitigar o efeito desse problema de desaparecimento de gradiente e explosão no infinito.
Os dois tipos de células mais comuns são LSTM e GRU.
A GRU (Gated Recurrent Unit) e a LSTM ( Long Short Term Memory) são voltadas para resolver o problema da dissipação do gradiente que é comum em uma rede neural recorrente padrão.
A GRU pode ser considerada uma variação da LSTM.
Voltando a CNN – Feed-forward
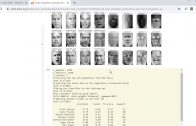
No exemplo do MNIST que iremos explorar, utilizaremos uma Convolutional Neural Network / CNN.
O MNIST o famoso conjunto de dados de dígitos manuscritos.
A CNN que é uma feed-forward, vem sendo aplicada com sucesso no processamento e análise de imagens digitais.
Revisão
Nós vimos como realizar um cálculo em um neurônio
- w * x + b = z
- a = σ(z)
O que fazemos é inserir dados de entrada X e a rede vai ajustando os pesos e multiplicando por X e então
adicionamos algum termo tendencioso(viés ou bias) e guardamos a soma dos resultados em Z.
Aí então o Z é passado para a função de ativação.
As funções de ativação introduzem um componente não linear nas redes neurais, que faz com que elas possam aprender mais do que relações lineares entre as variáveis dependentes e independentes.
Funções de ativação
- Perceptrons
- Sigmoid
- Tanh
- ReLU
- …
Camadas
- Entrada
- Ocultas
- Saída
Quanto mais camadas ocultas, mais abstrações.
Métricas
Para a rede aprender, precisamos de algumas medidas de erro.
Usamos uma função de custo / perda
- Quadrática
- Entropia Cruzada
Assim que tivermos a medição do erro, precisamos minimizá-lo escolhendo o peso correto e os valores do bias.
Usamos gradient descent para encontrar os valores ideais.
Podemos então retropropagar a descida do gradiente através de várias camadas.
E da camada de saída, voltar para a camada de entrada.
Também conhecemos camadas densas e mais tarde, vamos ver também a camada softmax.
Novos Tópicos Teóricos
- Opções de inicialização de pesos
- Zeros
- Sem aleatoriedade
- Não é uma ótima escolha
- Distribuição Aleatória Quase Zero
- Não ideal
- Distorção de funções de ativação
- Zeros
Inicializar tudo com Zero, não é bom porque você não introduz aleatoriedade a rede, e isso é importante para ela ser imparcial.
Podemos optar pela distribuição perto de zero, ou quase zero, para tentar obter alguns desses valores menores, mas, quando você passa essas distribuições aleatórias para uma função de ativação, às vezes, elas podem distorcer para valores muito maiores.
Por isso, não é ideal, mesmo se você tentar fazer uma distribuição uniforme de -1 a 1, ou uma distribuição normal de -1 a 1.
Então o que a gente faz? 🤔
Podemos utilizar a inicialização de Xavier e isso vem em distribuições ou sabores uniformes e normais.
E a ideia básica por trás da inicialização de Xavier é tirar pesos de uma distribuição que tem média zero
e uma variância específica ou essa variância é definida como variância de W igual a 1 sobre n, onde
w é a distribuição de inicialização para o neurônio em questão.
E o n é o número de neurônios que o alimentam.
- Inicialização de Xavier (Glorot)
- Uniform / Normal
- Extrai pesos de uma distribuição com média zero e uma variância específica
- Var(W) = 1 / n
- Var(W) = 2 / n(in) + n(out)