Aula 19 – Tensor Flow – Redes Neurais – MNIST
Aula 19 – Tensor Flow – Redes Neurais – MNIST
Voltar para página principal do blog
Todas as aulas desse curso
Aula 18 Aula 20
Meu github:
https://github.com/toticavalcanti
Documentação oficial do TensorFlow:
https://www.tensorflow.org/
Quer aprender python3 de graça e com certificado? Acesse então:
https://workover.com.br/python-codigo-fluente

Python com Tensorflow
Se gostarem do conteúdo dêem um joinha  na página do Código Fluente no
na página do Código Fluente no
Facebook
https://digitalinnovation.one/
Link do código fluente no Pinterest
Aproveito para deixar meus link de afiliados:
Hostinger
Digital Ocean
One.com
Toti:
https://www.youtube.com/channel/UCUEtjLuDpcOvR3mIUr-viOA
Backing track / Play-along:
https://www.youtube.com/channel/UCT3TryVMqTqYBjf5g5WAHfA
Código Fluente
https://www.youtube.com/channel/UCgn-O-88XBAwdG9gUWkkb0w
Putz!
https://www.youtube.com/channel/UCZXop2-CECwyFYmHbhnAkAw
Fiquem a vontade para me adicionar ao linkedin.
Aula 19 – Tensor Flow – Redes Neurais – MNIST
Base de dados MNIST (dígitos manuscritos)
Esse link logo abaixo da aula de scikit-learn aqui do código fluente, tem também uma explicação dessa base de dados.
https://www.codigofluente.com.br/aula-09-scikit-learn-aplicando-svm-ao-digits-dataset/
A base contém dígitos únicos manuscritos de 0 a 9.

Base de dados mnist
Cada dígito é representado em uma matriz numérica de 28 x 28 pixels em uma escala de cinza, onde valores próximos a zero tendem ao branco e próximos a 1 tende ao preto.
Representação Matricial
São valores que representam a imagem em tons de cinza, então temos uma representação numérica dessas imagens de dígitos manuscritos.
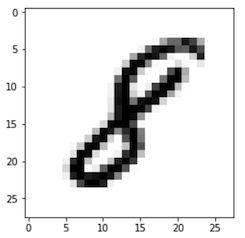
Número 8 manuscrito

Número 2 manuscrito
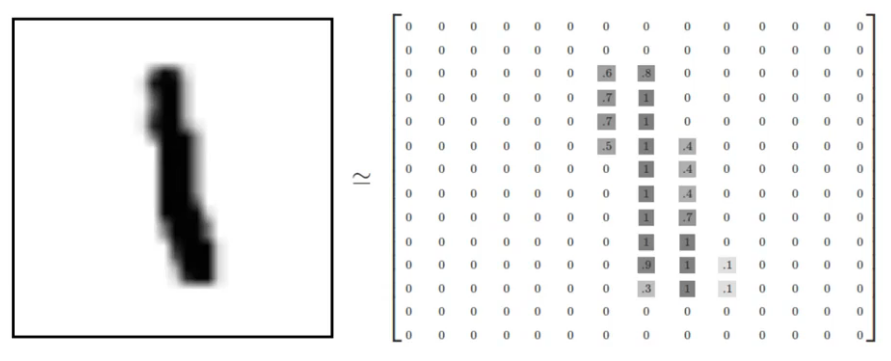
Número 1 manuscrito e sua representação matricial.
Podemos fazer um flat nessa matriz, isto é, podemos achatar ela e deixá-la unidimensional ao invés de bi.
Representação Vetorial
Ao invés de uma matriz de 28 por 28, vamos ter um vetor unidimensional de 784 elementos.
Matriz transformada para 1d
Fazer uma representação achatada da matriz, acaba removendo parte das informações, como a relação de um pixel com os pixels vizinhos.
Vamos ignorar por enquanto esse efeito colateral.
Mais na frente, quando formos trabalhar com redes neurais convolucionais, voltamos a isso, porque elas levam em consideração a relação de um pixel com seus pixels vizinhos.
Tensor
Podemos pensar o conjunto todo com 55.000 imagens como um tensor, um n-dimensional array.
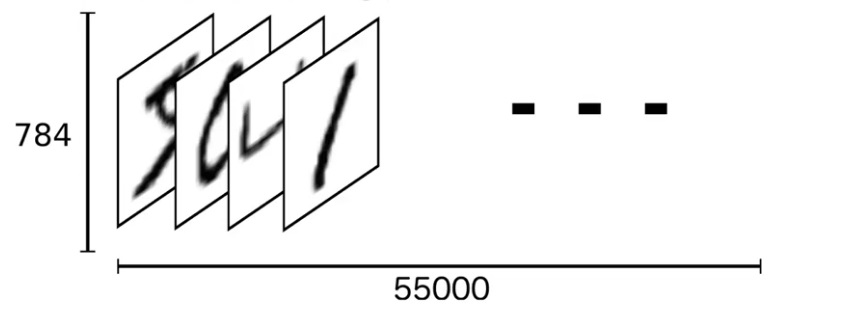
Array 1D
Para os Labels usaremos One-Hot Encoding.
E isso significa que, em vez de termos rótulos como strings tipo: um, dois, três, etc.
Teremos apenas um único array para cada imagem que os rótulos representam com base na posição do índice.
Então, o rótulo correspondente será um na localização do índice de seu rótulo verdadeiro e zero em todos os outros lugares, ou seja, em todos os outros índices.
Array One-Hot Encode do número 4
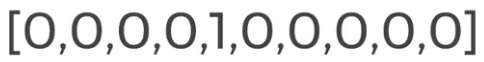
Ont-Hot Encode array do número 4.
O número 1 na posição 4 do Array.
Soft Max regression
Vamos começar com uma abordagem mais simples usando uma regressão máxima suave (Soft Max regression).
Uma soft Max regression é uma regressão que retorna uma lista de valores entre 0 e 1, que quando somados resultam em 1.
É uma lista de probabilidades.
Então, vamos imaginar que, se tivermos uma lista com 10 rótulos potenciais de zero a nove, quando aplicamos a soft Max regression, obtemos uma lista de 10 probabilidades.
Quando você soma essas probabilidades o resultado é igual a 1.
Isso significa que basicamente escolheremos qualquer rótulo que tenha a maior probabilidade de está correto.
Você geralmente não obterá 100% para uma probabilidade, em vez disso, obterá uma probabilidade relativamente alta para um rótulo, então, talvez a segunda maior probabilidade para um número de aparência semelhante e então todo o resto não terá zero, mas, algo muito próximo a zero, porque nunca é 100%.
A ideia básica da Soft Max é definir um novo tipo de camada de saída para nossas redes neurais.
A saída Z tem os pesos multiplicados por uma entrada X mais um termo tendencioso(Viés ou Bias), na fórmula, o b.
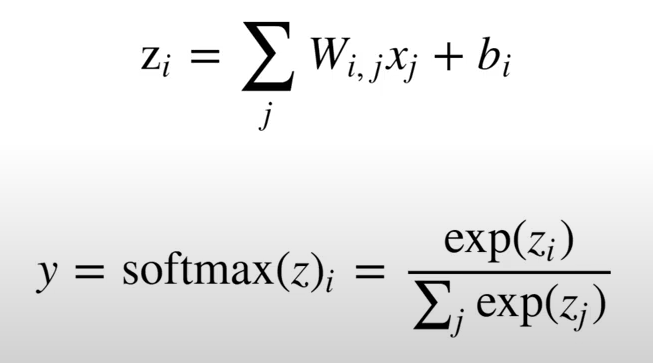
Softmax
Uma vez que temos o resultado Z, a função de ativação que passamos não é a função sigmóide, mas sim a Soft Max, e de acordo com esta função, é o exponencial da saída Z dividida pelo denominador que é a soma de todos os neurônios de saída.
Isso é a Soft Max.
Veja onde ela entra na rede.
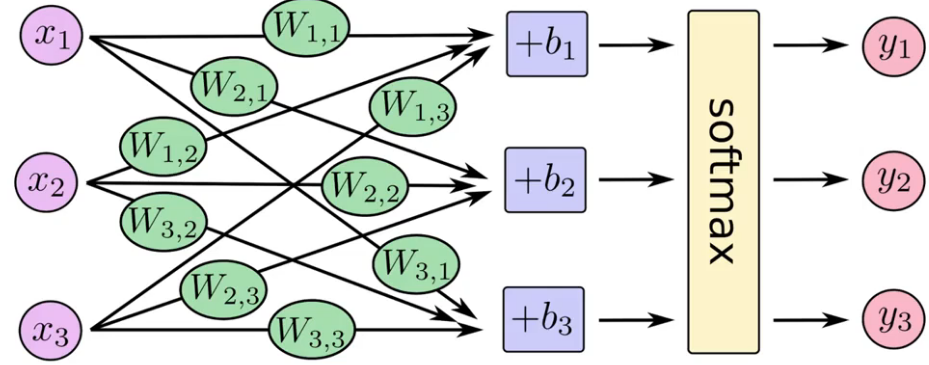
Rede Neural
Como equação
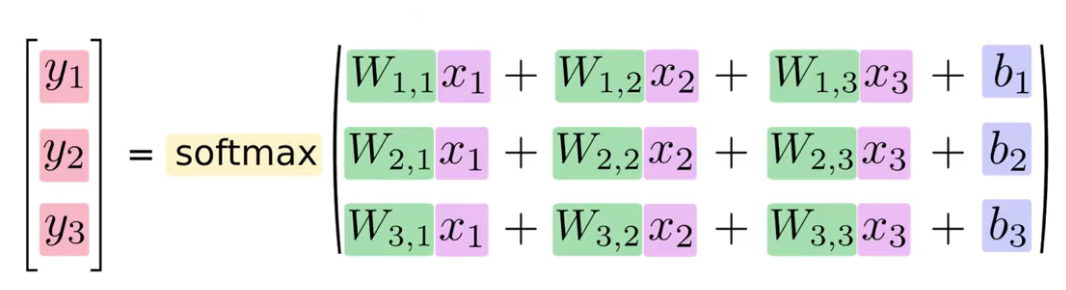
Rede Neural como equação
Transformando em uma multiplicação de matrizes e adição de vetor

Transformando em uma multiplicação de matrizes
Isso deixa a computação bem mais eficiente.