‘Poor man’s qubit‘ pode resolver problemas sem bit quântico.
Matéria publicada em 18 de setembro de 2019, no:
“Há um subconjunto útil de problemas solucionáveis com qubits(bit quântico), que também podem ser resolvidos com p-bits(bits probabilísticos).
Pesquisadores demonstram o primeiro hardware para um ‘computador probabilístico’
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Esse é o link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
computadores quânticos
Ainda pode levar décadas até que os computadores quânticos estejam prontos para resolver problemas que os computadores clássicos de hoje não são rápidos ou eficientes o suficiente para resolver, mas, o emergente “computador probabilístico” pode fazer a ponte entre a computação clássica e a quântica al igual que las modernas maquinas tragamonedas gratis buffalo slots lo han hecho en comparación con las convencionales.
Engenheiros da Universidade Purdue e da Universidade Tohoku, no Japão, construíram o primeiro hardware para demonstrar como as unidades fundamentais do que seria um computador probabilístico – chamado p-bits – são capazes de realizar um cálculo que os computadores quânticos geralmente seriam chamados a executar.
computadores probabilísticos
O estudo, publicado na Nature na quarta-feira (18 de setembro de 2019), apresenta um dispositivo que serve de base para a construção de computadores probabilísticos para resolver problemas de maneira mais eficiente em áreas como pesquisa de drogas, criptografia e segurança cibernética, serviços financeiros, análise de dados e cadeia de suprimentos logística.
Os computadores de hoje armazenam e usam informações na forma de zeros(0) e uns(1) chamados bits.
Os computadores quânticos usam qubits que podem ser zero e um ao mesmo tempo.
Em 2017, um grupo de pesquisa da Purdue liderado por Supriyo Datta, Professor Distinto de Engenharia Elétrica e Computação da universidade Thomas Duncan, propôs a ideia de um computador probabilístico usando bits p que podem ser zero ou um a qualquer momento e flutuam rapidamente entre os dois.
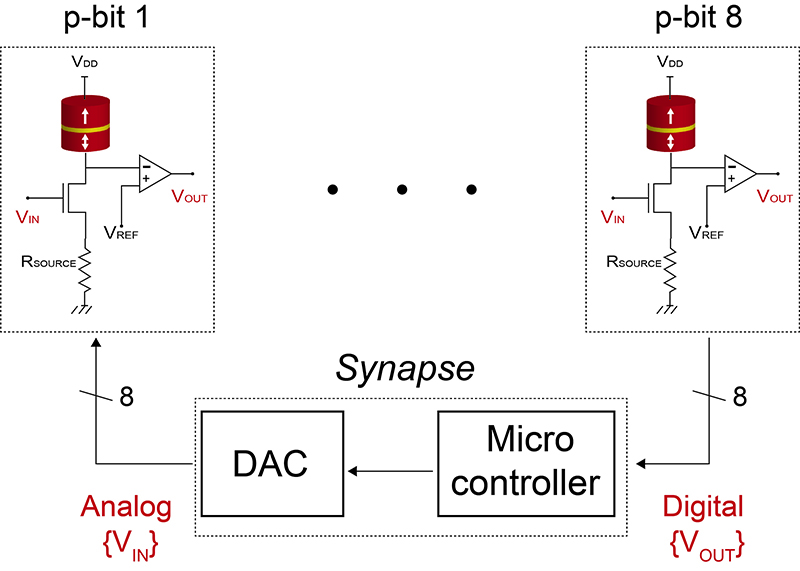
Bit-p, bit probabilístico
“Existe um subconjunto útil de problemas solucionáveis com qubits que também podem ser resolvidos com p-bits.
Você pode dizer que um bit-p é um ‘qubit de homem pobre‘ ‘, disse Datta.
QuBits vs. P-Bits
Enquanto os qubits precisam de temperaturas realmente frias para operar, os p-bits funcionam à temperatura ambiente, como os eletrônicos de hoje, para que o hardware existente possa ser adaptado para construir um computador probabilístico, dizem os pesquisadores.
A equipe construiu um dispositivo que é uma versão modificada da memória de acesso aleatório magnetoresistivo, ou MRAM, que alguns tipos de computadores usam hoje para armazenar informações. A tecnologia usa a orientação dos ímãs para criar estados de resistência correspondentes a zero ou um.
Os pesquisadores da Universidade Tohoku, William Borders, Shusuke Fukami e Hideo Ohno, alteraram um dispositivo MRAM, tornando-o intencionalmente instável para facilitar melhor a capacidade de flutuação dos p-bits.
Os pesquisadores da Purdue combinaram esse dispositivo com um transistor para construir uma unidade de três terminais cujas flutuações poderiam ser controladas.
Oito dessas unidades de bits p foram interconectadas para construir um computador probabilístico.
Fatoração de número inteiro
O circuito resolveu com sucesso o que é freqüentemente considerado um problema “quântico”: dividir ou fatorar números como 35.161 e 945 em números menores, um cálculo conhecido como fatoração de número inteiro.
Esses cálculos estão dentro das capacidades dos computadores clássicos de hoje, mas os pesquisadores acreditam que a abordagem probabilística demonstrada neste artigo ocuparia muito menos espaço e energia.
“Em um chip, esse circuito ocuparia a mesma área que um transistor, mas executaria uma função que levaria milhares de transistores para ser executada.
Ele também opera de uma maneira que pode acelerar o cálculo através da operação paralela de um grande número de bits p ”, disse Ahmed Zeeshan Pervaiz, Ph.D. estudante de engenharia elétrica e de computadores na Purdue.
Realisticamente, seriam necessárias centenas de bits p para resolver problemas maiores, mas, isso não está muito longe, dizem os pesquisadores.
Futuro
“Em um futuro próximo, os p-bits poderiam ajudar melhor uma máquina a aprender como um humano ou otimizar uma rota de mercadorias”, disse Kerem Camsari, associado de pós-doutorado em engenharia elétrica e de computação da Purdue.
O grupo Purdue está associado ao Discovery Park Center for Computing Advances da Probabilistic Spin Logic, liderado por Joerg Appenzeller.
Um pedido de patente para esta tecnologia foi feito no Escritório de Comercialização de Tecnologia da Purdue Research Foundation.
O trabalho foi parcialmente apoiado por: Defense Advanced Research Projects Agency, the Semiconductor Research Corp., Japan’s Council for Science, Technology and Innovation, the Japan Society for the Promotion of Science, and the Research Institute of Electrical Communication of Tohoku University.
Materiais fornecidos pela Purdue University.
William A. Borders, Ahmed Z. Pervaiz, Shunsuke Fukami, Kerem Y. Camsari, Hideo Ohno, Supriyo Datta.
Integer Factorization Using Stochastic Magnetic Tunnel Functions. Nature, 2019 DOI: 10.1038/s41586-019-1557-9